❤
npm
Sign UpSign In

quantum-circuit

0.9.222 • Public • Published

Quantum Circuit Simulator

quantum-circuit is open source quantum circuit simulator implemented in javascript. Smoothly runs 20+ qubit simulations in browser or at server (node.js). You can use it in your javascript program to run quantum simulations.

Circuit can be imported from OpenQASM, Quil and IONQ. You can export circuits to OpenQASM, pyQuil, Quil, Qiskit, Cirq, TensorFlow Quantum, QSharp, and QuEST, so it can be used for conversion between quantum programming languages. Circuit drawing can be exported to SVG vector image.

Live examples

Quantum Programming Studio

Quantum Programming Studio is web based quantum programming IDE and simulator built on top of this package. Circuit can be executed on real quantum computer directly from the UI.

Other live examples

Using in browser

Simply include quantum-circuit.min.js into your html page (available via unpkg CDN https://unpkg.com/quantum-circuit)

<!doctype html>
<html>
    <head>
        <title>Quantum Circuit Simulator Example</title>
    </head>

    <body>
        <script type="text/javascript" src="https://unpkg.com/quantum-circuit"></script>

        <script type="text/javascript">
            // Your code here
        </script>
    </body>
</html>

Using at server with node.js

Add quantum-circuit npm module to your node.js project:

npm install --save quantum-circuit

And then import it into your program:

var QuantumCircuit = require("quantum-circuit");

// Your code here

Node.js examples

See /example/nodejs directory.

Using with Jupyter notebook

You need to install ijavascript kernel for Jupyter notebook

You can install quantum-circuit npm module globally and invoke jupyter notebook from any directory:

npm install -g quantum-circuit

Or inside new directory do:

npm init
npm install --save quantum-circuit
jupyter notebook

Jupyter notebook examples

See /example/jupyter directory.

Getting started

Create circuit

Create instance of QuantumCircuit class, optionally passing number of qubits (wires) to constructor:

var circuit = new QuantumCircuit(3);

Note: number of qubits is optional argument - circuit will expand automatically if you add gates to non-existing wires

Add single-qubit gates

Call addGate method passing gate name, column index and qubit (wire) index:

circuit.addGate(gateName, column, wire);

For example, to add Hadamard gate as a first gate (column 0) at second qubit (wire 1) type:

circuit.addGate("h", 0, 1);

Result is:

                  
         Column 0 
                  
Wire 0 -----------
                  
          |---|   
Wire 1 ---| H |---
          |---|

Note: if column is negative integer then gate will be added to the end of the wire

Add multi-qubit gates

Call addGate method passing gate name, column index and array of connected qubits (wires):

circuit.addGate(gateName, column, arrayOfWires);

For example, to add CNOT as a second gate (column 1) controlled by second qubit (wire 1) at third qubit as target (wire 2) do:

circuit.addGate("cx", 1, [1, 2]);
                                
         Column 0    Column 1   
                               
Wire 0 ------------------------
                               
                               
Wire 1 -----------------o------
                        |      
                     |-----|   
Wire 2 --------------| CX  |---
                     |-----|

Note: if column is negative integer then gate will be added to the end

Example - Quantum random number generator

var QuantumCircuit = require("quantum-circuit");

//
// 8-bit quantum random number generator
//

var quantumRandom = function() {

    var circuit = new QuantumCircuit();

    for(var i = 0; i < 8; i++) {
        //
        // add Hadamard gate to the end (-1) of i-th wire
        //
        circuit.addGate("h", -1, i);

        //
        // add measurement gate to i-th qubit which will store result 
        // into classical register "c", into i-th classical bit
        //
        circuit.addMeasure(i, "c", i); 
    }

    // run circuit
    circuit.run();

    // return value of register "c"
    return circuit.getCregValue("c");
};

// Usage - print random number to terminal
console.log(quantumRandom());

Implemented gates

Name pyQuil Cirq Q# IONQ Qubits Params Description
id I I I 1 Single qubit identity gate
x X X X x 1 Pauli X (PI rotation over X-axis) aka "NOT" gate
y Y Y Y y 1 Pauli Y (PI rotation over Y-axis)
z Z Z Z z 1 Pauli Z (PI rotation over Z-axis)
h H H H h 1 Hadamard gate
srn def srn X**(1/2) v 1 Square root of NOT
srndg def srndg X**(-1/2) vi 1 Inverse square root of NOT
r2 S S S 1 PI/2 rotation over Z-axis aka "Phase PI/2"
r4 T T T 1 PI/4 rotation over Z-axis aka "Phase PI/4"
r8 PHASE(pi/8) u1(pi/8) 1 PI/8 rotation over Z-axis aka "Phase PI/8"
rx RX rx Rx rx 1 theta Rotation around the X-axis by given angle
ry RY ry Ry ry 1 theta Rotation around the Y-axis by given angle
rz RZ rz Rz rz 1 phi Rotation around the Z-axis by given angle
u1 PHASE def u1 1 lambda Single-qubit rotation about the Z axis
u2 def u2 def u2 1 phi, lambda Single-qubit rotation about the X+Z axis
u3 def u3 def u3 1 theta, phi, lambda Generic single-qubit rotation gate with 3 Euler angles
s S S S s 1 PI/2 rotation over Z-axis (synonym for r2)
t T T T t 1 PI/4 rotation over Z-axis (synonym for r4)
sdg PHASE(-pi/2) u1(-pi/2) si 1 (-PI/2) rotation over Z-axis
tdg PHASE(-pi/4) u1(-pi/4) ti 1 (-PI/4) rotation over Z-axis
gpi def gpi gpi gpi 1 phi GPi gate
gpi2 def gpi2 gpi2 gpi2 1 phi GPi2 gate
vz def vz vz vz 1 theta VirtualZ gate
cx CNOT CNOT CNOT cnot 2 Controlled NOT (CNOT) gate
cy def cy Y Controlled Y 2 Controlled Y gate (controlled rotation over Y-axis by PI)
cz CZ CZ Controlled Z 2 Controlled Z gate (controlled rotation over Z-axis by PI)
ch def ch H Controlled H 2 Controlled Hadamard gate
csrn def csrn X**(1/2) 2 Controlled square root of NOT
swap SWAP SWAP SWAP swap 2 Swaps the state of two qubits.
srswap def srswap SWAP**(1/2) 2 Square root of swap
iswap ISWAP ISWAP 2 Swaps the state of two qubits, applying a -i phase to q1 when it is in the 1 state and a -i phase to q2 when it is in the 0 state
xx def xx xx xx 2 theta XX gate
yy def yy YY yy 2 theta YY gate
zz def zz zz 2 theta Parametric 2-qubit rotation about ZZ
xy XY def xy 2 phi XY gate
ms def ms ms ms 2 phi0, phi1 Mølmer-Sørensen gate
cr2 CPHASE(pi/2) cu1(pi/2) 2 Controlled PI/2 rotation over Z-axis
cr4 CPHASE(pi/4) cu1(pi/4) 2 Controlled PI/4 rotation over Z-axis
cr8 CPHASE(pi/8) cu1(pi/8) 2 Controlled PI/8 rotation over Z-axis
crx def crx rx(theta) Controlled Rx 2 theta Controlled rotation around the X-axis by given angle
cry def cry ry(theta) Controlled Ry 2 theta Controlled rotation around the Y-axis by given angle
crz def crz rz(phi) Controlled Rz 2 phi Controlled rotation around the Z-axis by given angle
cu1 CPHASE def cu1 2 lambda Controlled rotation about the Z axis
cu2 def cu2 def cu2 2 phi, lambda Controlled rotation about the X+Z axis
cu3 def cu3 def cu3 2 theta, phi, lambda Controlled rotation gate with 3 Euler angles
cs CPHASE(pi/2) cu1(pi/2) 2 Controlled PI/2 rotation over Z-axis (synonym for cr2)
ct CPHASE(pi/4) cu1(pi/4) 2 Controlled PI/4 rotation over Z-axis (synonym for cr4)
csdg CPHASE(-pi/2) cu1(-pi/2) 2 Controlled (-PI/2) rotation over Z-axis
ctdg CPHASE(-pi/4) cu1(-pi/4) 2 Controlled (-PI/4) rotation over Z-axis
ccx CCNOT CCX CCNOT 3 Toffoli aka "CCNOT" gate
cswap CSWAP CSWAP Controlled SWAP 3 Controlled swap aka "Fredkin" gate
csrswap def csrswap SWAP**(1/2) 3 Controlled square root of swap
reset RESET reset Reset 1 Resets qubit
measure MEASURE measure M 1 Measures qubit and stores chance (0 or 1) into classical bit

For more details see gate reference

Run circuit

Simply call run method.

circuit.run();

Initial state

By default, initial state of each qubit is |0>. You can pass initial values as array of bool (true or false) or integers (0 or 1). This will set first two qubits to |1> and evaluate circuit:

circuit.run([1, 1]);

Measurement

Method probabilities() will return array of probabilities (real numbers between 0 and 1) for each qubit:

console.log(circuit.probabilities());

Method probability(wire) will return probability (real number between 0 and 1) for given qubit:

console.log(circuit.probability(0));

Method measureAll() returns array of chances (as integers 0 or 1) for each qubit:

Example:

console.log(circuit.measureAll());

Method measure(wire) returns chance (as integer 0 or 1) for given qubit:

Example:

console.log(circuit.measure(0));

You can store measurement into classical register. For example, to measure first qubit (wire 0) and store result into classical register named c as fourth bit (bit 3):

circuit.measure(0, "c", 3);

You can add measure gate to circuit and then measurement will be done automatically and result will be stored into classical register:

circuit.addGate("measure", -1, 0, { creg: { name: "c", bit: 3 } });

Short form of writing this is addMeasure(wire, creg, cbit):

circuit.addMeasure(0, "c", 3);

Note:

  • Measurement gate will reset qubit to measured value only if there are gates with classical control (gates controlled by classical registers). Otherwise, measurement gate will leave qubit as is - measured value will be written to classical register and qubit will remain unchanged. This "nondestructive" behavior is handy when experimenting. However, it will automatically switches to "destructive" mode when needed (when classical control is present)

  • If specified classical register doesn't exists - it will be created automatically.

Classical registers

Create register

Classical registers are created automatically if you add measurement gate to the circuit but you can also manually create registers by calling createCreg(name, len).

Example: create classical 5-bit register named ans:

circuit.createCreg("ans", 5);

Read register

To get register value as integer, call getCregValue(name).

Example:

var value = circuit.getCregValue("ans");

Read all registers as dictionary

var regs = circuit.getCregs();
console.log(regs);

Read all registers as tab delimited CSV string

var tsv = circuit.cregsAsString();
console.log(tsv);

Read single bit

Example: get bit 3 from register named ans:

console.log(circuit.getCregBit("ans", 3));

Returns integer: 0 or 1

Set single bit

Example: set bit 3 to 1 in register named ans:

circuit.setCregBit("ans", 3, 1);

Control by classical register

Each quatum gate in the circuit (except "measure" gate) can be controlled by classical register - gate will be executed only if classical register contains specified value. Pass options object as fourth argument to addGate method:

Example:

circuit.addGate("x", -1, 0, { 
    condition: { 
        creg: "ans",
        value: 7
    }
});

In this example, "x" gate will execute on qubit 0 only if value of register named "ans" equals 7.

Reset qubit

You can reset qubit to value |0> or |1> with resetQubit method:

circuit.resetQubit(3, 0);

In this example, qubit 3 will be set to 0|>.

Note that all entangled qubits will be changed as well

View/print state vector

You can get state as string with method stateAsString(onlyPossible):

var s = circuit.stateAsString(false);

If you want only possible values (only values with probability > 0) then pass true:

var s = circuit.stateAsString(true);

Or, you can print state to javascript console with method print(onlyPossible):

circuit.print(false);

If you want to print only possible values (only values with probability > 0) then pass true:

var s = circuit.print(true);

Save/Load circuit

You can export circuit to javascript object (format internally used by QuantumCircuit) by calling save method:

var obj = circuit.save();

// now do something with obj, save to file or whatever...

And load previously saved circuit by calling load method:

var obj = // ...load object from file or from another circuit or whatever

circuit.load(obj);

Use circuit as a gate in another circuit

You can "compile" any circuit and use it as a gate in another circuit like this:

// export circuit to variable
var obj = someCircuit.save();

// register it as a gate in another circuit
anotherCircuit.registerGate("my_gate", obj);

// use it as a gate in another circuit
// assuming original circuit has three qubits then gate must spread to 3 qubits, in this example: 2, 3, 4)
anotherCircuit.addGate("my_gate", 0, [2, 3, 4]);

Decompose circuit

If your circuit contains user defined gates (created from another circuit), you can decompose it into equivalent circuit containing only basic gates.

If you pass true as argument to function save, you'll get decomposed circuit.

Example:

var obj = circuit.save(true);
// now obj contains decomposed circuit. You can load it:
circuit.load(obj);

Import circuit

Import from QASM

Circuit can be imported from OpenQASM with following limitations:

  • import directive is ignored (but most of gates defined in qelib1.inc are supported) TODO

  • barrier is ignored. TODO

  • reset is ignored. TODO

To import circuit from OpenQASM use importQASM(input, errorCallback) method:

Example:

circuit.importQASM("OPENQASM 2.0;\nimport \"qelib1.inc\";\nqreg q[2];\nh q[0];\ncx q[0],q[1];\n", function(errors) {
    console.log(errors);
});

  • input is string containing QASM source code.

  • errorCallback (optional) callback will be called after parsing with one argument: array containing errors or empty array on success. If no callback is provided, function will throw error if input contains errors.

Import from QUIL

Circuit can be imported from Quil:

To import circuit from QUIL use importQuil(quil, errorCallback, options, qubitNames, renamedGates, lineOffset) method:

Example:

circuit.importQuil("H 0\nCNOT 0 1\n", function(errors) {
    console.log(errors);
});

  • quil is string containing QUIL source code.

  • errorCallback (optional) callback will be called after parsing with one argument: array containing errors or empty array on success. If no callback is provided, function will throw error if input contains errors.

  • options (optional) function will be called after parsing with array containing syntax errors.

  • qubitNames (optional) names to be given to the qubits.

  • renamedGates (optional) custom names given to basic commands

  • lineOffset (optional) no. of spaces before a new line

Import from Qobj

Circuit can be imported from Qobj:

To import circuit from OpenQASM use importQobj(qobj, errorCallback) method:

Example:

circuit.importQobj({"qobj_id":"qobj_WlLkcGHxihyqWGrKEZ","type":"QASM","schema_version":"1.0","experiments":[{"header":{"memory_slots":0,"n_qubits":2,"qreg_sizes":[["q",2]],"qubit_labels":[["q",0],["q",1]],"creg_sizes":[],"clbit_labels":[],"name":"circuit0","description":"text_exp"},"config":{"n_qubits":2,"memory_slots":0},"instructions":[{"name":"x","qubits":[0,1]}]}],"header":{"description":"test_circ"},"config":{"shots":1,"memory_slots":0}}, function(errors) {
    console.log(errors);
});

  • qobj is Qobj JSON ("type": "QASM").

  • errorCallback (optional) callback will be called after parsing with one argument: array containing errors or empty array on success. If no callback is provided, function will throw error if input contains errors.

Import from IONQ json

Circuit can be imported from IONQ json:

To import circuit from IONQ json use importIonq(data, errorCallback) method:

Example:

var ionqCircuit = {
  "qubits": 2,
  "circuit": [
    {
      "gate": "h",
      "target": 0
    },
    {
      "gate": "cnot",
      "target": 1,
      "control": 0
    }
  ]
};

circuit.importIonq(ionqCircuit, function(errors) {
    console.log(errors);
});

  • data is IONQ JSON object.

  • errorCallback (optional) callback will be called after parsing with one argument: array containing errors or empty array on success. If no callback is provided, function will throw error if input contains errors.

Export circuit

Export to JavaScript

Circuit can be exported to JavaScript with exportJavaScript(comment, decompose, null, asJupyter) method:

Example:

var js = circuit.exportJavaScript("Comment to insert at the beginning.\nCan be multi-line comment like this one.", false);

  • comment - comment to insert at the beginning of the file.

  • decompose - if set to true and circuit contains user defined gates then it will be decomposed to basic gates and then exported. If set to false then user defined gates will exported as subroutines.

  • asJupyter - when this argument is true jupyter notebook (set to use ijavascript kernel) will be returned.

Export to python (Qiskit)

Circuit can be exported to Qiskit with following limitation:

  • User defined gates are not generated. Instead, circuit is decomposed to basic gates and exported. Effect is the same but code is less readable. TODO

  • Gates not directly supported by Qiskit are exported as-is - their definition is not generated. TODO

To export circuit to Qiskit use exportToQiskit(options, exportAsGateName, circuitReplacement, insideSubmodule) method :

Example:

var qiskit = circuit.exportToQiskit({comment:"Comment to insert at the beginning.\nCan be multi-line comment as this one."}, false, null, null);

  • options - consists of parameters for circuit export as follows:

    • comment - comment to insert at the beginning of the file.

    • decompose - if set to true and circuit contains user defined gates then it will be decomposed to basic gates and then exported. If set to false then user defined gates will exported as subroutines.

    • versionStr - Qiskit version. Can be "0.7". Exports to latest supported version when empty string is provided. Remember - it is a string.

    • providerName - name of the Qiskit backend simulator provider.

    • backendName - name of the Qiskit backend simulator.

    • asJupyter - when this argument is true jupyter notebook will be returned.

    • shots - no. of trials.

    • hybrid - when true exports user defined cost function along with circuit for hybrid Quantum-Classical Algorithms

  • insideSubmodule - when true adds extra indent for alignment

  • exportAsGateName - name of the custom gate containing the Qiskit circuit.

  • circuitReplacement - when true exports only gates in the circuit

(Deprecated. Please use exportToQiskit() instead)

To export circuit to Qiskit you can also use exportQiskit(comment, decompose, exportAsGateName, versionStr, providerName, backendName, asJupyter, shots, circuitReplacement, insideSubmodule, hybrid)

Example:

var qiskit = circuit.exportQiskit("Comment to insert at the beginning.\nCan be multi-line comment as this one.", false, null, null);

  • comment - comment to insert at the beginning of the file.

  • decompose - if set to true and circuit contains user defined gates then it will be decomposed to basic gates and then exported. If set to false then user defined gates will exported as subroutines.

  • versionStr - Qiskit version. Can be "0.7". Exports to latest supported version when empty string is provided. Remember - it is a string.

  • providerName - name of the Qiskit backend simulator provider.

  • backendName - name of the Qiskit backend simulator.

  • asJupyter - when this argument is true jupyter notebook will be returned.

  • shots - no. of trials.

  • hybrid - when true exports user defined cost function along with circuit for hybrid Quantum-Classical Algorithms

  • insideSubmodule - when true adds extra indent for alignment

  • exportAsGateName - name of the custom gate containing the Qiskit circuit.

  • circuitReplacement - when true exports only gates in the circuit

Export to QASM

Circuit can be exported to OpenQASM with following limitation:

  • at the moment, gates not directly supported by QASM and qelib1.inc are exported as-is - their definition is not generated. TODO

To export circuit to OpenQASM use exportToQASM(options, exportAsGateName, circuitReplacement, insideSubmodule) method:

Example:

var qasm = circuit.exportToQASM({comment:"Comment to insert at the beginning.\nCan be multi-line comment as this one."}, false);

  • options - consists of parameters for circuit export as follows:

    • comment - comment to insert at the beginning of the file.

    • decompose - if set to true and circuit contains user defined gates then it will be decomposed to basic gates and then exported. If set to false then user defined gates will exported as subroutines.

    • compatibilityMode - if set to true exports the circuit in compatible mode

  • insideSubmodule - when true adds extra indent for alignment

  • exportAsGateName - name of the custom gate containing the Qiskit circuit.

  • circuitReplacement - when true exports only gates in the circuit

(Deprecated. Please use exportToQASM() instead)

To export circuit to OpenQASM you can also use exportQASM(comment, decompose, exportAsGateName, circuitReplacement, compatibilityMode, insideSubmodule) method:

Example:

var qasm = circuit.exportQASM("Comment to insert at the beginning.\nCan be multi-line comment as this one.", false);

  • comment - comment to insert at the beginning of the file.

  • decompose - if set to true and circuit contains user defined gates then it will be decomposed to basic gates and then exported. If set to false then user defined gates will exported as subroutines.

  • exportAsGateName - name of the custom gate containing the Qiskit circuit.

  • circuitReplacement - when true exports only gates in the circuit

  • compatibilityMode - if set to true exports the circuit in compatible mode

  • insideSubmodule - when true adds extra indent for alignment

Export to python (pyQuil)

Circuit can be exported to pyQuil

To export circuit to pyQuil use exportToPyquil(options, exportAsGateName) method:

Example:

var qasm = circuit.exportToPyquil({comment:"Comment to insert at the beginning.\nCan be multi-line comment as this one."}, false);

  • options - consists of parameters for circuit export as follows:

    • comment - comment to insert at the beginning of the file.

    • decompose - if set to true and circuit contains user defined gates then it will be decomposed to basic gates and then exported. If set to false then user defined gates will exported as subroutines.

    • versionStr - pyQuil version. Can be "1.9", "2.0" or "2.1". Exports to latest supported version when empty string is provided. Remember - it is a string.

    • lattice - You can optionally pass then name of the lattice.

    • asQVM - If this argument is true (and if lattice is specified) then produced code will run on QVM mimicking running on QPU. Otherwise, produced code will run on QPU.

    • asJupyter - when this argument is true jupyter notebook will be returned.

    • shots - no. of trials.

    • hybrid - when true exports user defined cost function along with circuit for hybrid Quantum-Classical Algorithms

  • exportAsGateName - name of the custom gate containing the Pyquil circuit.

(Deprecated. Please use exportToPyquil() instead)

To export circuit to Pyquil you can also use exportPyquil(comment, decompose, exportAsGateName, versionStr, lattice, asQVM, asJupyter, shots, hybrid) method:

Example:

var pyquil = circuit.exportPyquil("Comment to insert at the beginning.\nCan be multi-line comment as this one.", false, null, "2.1", "", false);

  • comment - comment to insert at the beginning of the file.

  • decompose - if set to true and circuit contains user defined gates then it will be decomposed to basic gates and then exported. If set to false then user defined gates will exported as subroutines.

  • exportAsGateName - name of the custom gate containing the Pyquil circuit.

  • versionStr - pyQuil version. Can be "1.9", "2.0" or "2.1". Exports to latest supported version when empty string is provided. Remember - it is a string.

  • lattice - You can optionally pass then name of the lattice.

  • asQVM - If this argument is true (and if lattice is specified) then produced code will run on QVM mimicking running on QPU. Otherwise, produced code will run on QPU.

  • asJupyter - when this argument is true jupyter notebook will be returned.

  • shots - no. of trials.

  • hybrid - when true exports user defined cost function along with circuit for hybrid Quantum-Classical Algorithms

Export to Quil

Circuit can be exported to Quil

To export circuit to Quil use exportToQuil(options, exportAsGateName) method:

Example:

var quil = circuit.exportToQuil({comment:"Comment to insert at the beginning.\nCan be multi-line comment as this one."}, false);

  • options - consists of parameters for circuit export as follows:

    • comment - comment to insert at the beginning of the file.

    • decompose - if set to true and circuit contains user defined gates then it will be decomposed to basic gates and then exported. If set to false then user defined gates will exported as subroutines.

    • versionStr - pyQuil version. Can be "1.9", "2.0" or "2.1". Exports to latest supported version when empty string is provided. Remember - it is a string.

  • exportAsGateName - name of the custom gate containing the Pyquil circuit.

(Deprecated. Please use exportToQuil() instead)

To export circuit to Quil you can also use exportQuil(comment, decompose, exportAsGateName, versionStr) method:

Example:

var quil = circuit.exportQuil("Comment to insert at the beginning.\nCan be multi-line comment as this one.", false, null, "2.0");

  • comment - comment to insert at the beginning of the file.

  • decompose - if set to true and circuit contains user defined gates then it will be decomposed to basic gates and then exported. If set to false then user defined gates will exported as subroutines (DEFCIRCUIT).

  • exportAsGateName - name of the custom gate containing the Quil circuit.

  • versionStr - Quil version. Can be "1.0" or "2.0" or empty string. Exports to latest supported version when empty string is provided. Remember - it is a string.

Export to python (Cirq)

Circuit can be exported to Cirq with following limitation:

  • Gates not directly supported by Cirq are exported as-is - their definition is not generated. TODO

  • Classical control is ignored (comment with warning is generated). TODO

To export circuit to Cirq use exportToCirq(options, exportAsGateName) method:

Example:

var cirq = circuit.exportToCirq({comment:"Comment to insert at the beginning.\nCan be multi-line comment as this one."}, false);

  • options - consists of parameters for circuit export as follows:

    • comment - comment to insert at the beginning of the file.

    • decompose - if set to true and circuit contains user defined gates then it will be decomposed to basic gates and then exported. If set to false then user defined gates will exported as subroutines.

    • versionStr - Cirq version. Can be "0.5" or empty string. Exports to latest supported version when empty string is provided. Remember - it is a string.

    • asJupyter - when this argument is true jupyter notebook will be returned.

    • shots - no. of trials.

    • exportTfq - if set to true the export function will export circuit to Tensorflow Quantum.

  • exportAsGateName - name of the custom gate containing the Cirq circuit.

(Deprecated. Please use exportToCirq() instead)

To export circuit to Cirq you can also use exportCirq(comment, decompose, exportAsGateName, versionStr, asJupyter, shots, exportTfq) method:

Example:

var cirq = circuit.exportCirq("Comment to insert at the beginning.\nCan be multi-line comment as this one.", false, null, null, false, null, false);

  • comment - comment to insert at the beginning of the file.

  • decompose - if set to true and circuit contains user defined gates then it will be decomposed to basic gates and then exported. If set to false then user defined gates will exported as subroutines.

  • exportAsGateName - name of the custom gate containing the Cirq circuit.

  • versionStr - Cirq version. Can be "0.5" or empty string. Exports to latest supported version when empty string is provided. Remember - it is a string.

  • asJupyter - when this argument is true jupyter notebook will be returned.

  • shots - no. of trials.

  • exportTfq - if set to true the export function will export circuit to Tensorflow Quantum.

Export to C/C++ (QuEST)

Circuit can be exported to QuEST

To export circuit to QuEST use exportQuEST(newOptions, exportAsGateName, definedFunc) method:

Example:

var quest = circuit.exportToQuEST("Comment to insert at the beginning.\nCan be multi-line comment as this one.", false);

  • options - consists of parameters for circuit export as follows:

    • comment - comment to insert at the beginning of the file.

    • decompose - if set to true and circuit contains user defined gates then it will be decomposed to basic gates and then exported. If set to false then user defined gates will exported as subroutines.

  • exportAsGateName - name of the custom gate containing the Cirq circuit.

  • definedFunc - list of gates that must be present in the defined function

(Deprecated. Please use exportToQuEST() instead)

To export circuit to QuEST you can also use exportQuEST(comment, decompose, exportAsGateName, definedFunc) method:

Example:

var quest = circuit.exportQuEST("Comment to insert at the beginning.\nCan be multi-line comment as this one.", false, null, null);

  • comment - comment to insert at the beginning of the file.

  • decompose - if set to true and circuit contains user defined gates then it will be decomposed to basic gates and then exported. If set to false then user defined gates will exported as subroutines.

  • exportAsGateName - name of the custom gate containing the QuEST circuit.

  • definedFunc - list of gates that must be present in the defined function

Export to Q# (QSharp)

Circuit can be exported to Q#.

To export circuit to Q# use exportQSharp(options, exportAsGateName) method:

Example:

var qsharp = circuit.exportQSharp("Comment to insert at the beginning.\nCan be multi-line comment as this one.", false, null, null, false, null);

  • options - consists of parameters for circuit export as follows:

    • comment - comment to insert at the beginning of the file.

    • decompose - if set to true and circuit contains user defined gates then it will be decomposed to basic gates and then exported. If set to false then user defined gates will exported as subroutines.

    • versionStr - QSharp version. Can be "0.1" or empty string. Exports to latest supported version when empty string is provided. Remember - it is a string.

    • asJupyter - when this argument is true jupyter notebook (set to use qsharp kernel) will be returned.

    • circuitName - Name of the circuit that is being exported to QSharp. By default set to "Circuit"

    • indentDepth - The no. of tabs to be put before a Python line of code.

  • exportAsGateName - name of the custom gate containing the QSharp circuit.

(Deprecated. Please use exportToQSharp() instead)

To export circuit to Q# use exportQSharp(comment, decompose, exportAsGateName, versionStr, asJupyter, circuitName, indentDepth) method:

Example:

var qsharp = circuit.exportQSharp("Comment to insert at the beginning.\nCan be multi-line comment as this one.", false, null, null, false, null);

  • comment - comment to insert at the beginning of the file.

  • decompose - if set to true and circuit contains user defined gates then it will be decomposed to basic gates and then exported. If set to false then user defined gates will exported as subroutines.

  • exportAsGateName - name of the custom gate containing the QSharp circuit.

  • versionStr - QSharp version. Can be "0.1" or empty string. Exports to latest supported version when empty string is provided. Remember - it is a string.

  • asJupyter - when this argument is true jupyter notebook (set to use qsharp kernel) will be returned.

  • circuitName - Name of the circuit that is being exported to QSharp. By default set to "Circuit"

  • indentDepth - The no. of tabs to be put before a Python line of code.

Export to Qobj

Circuit can be exported to Qobj:

To export circuit to Qiskit use exportToQobj(options, circuitReplacement) method :

Example:

var qobj = circuit.exportToQobj({circuitName:"new_circuit"}, false);

  • options - consists of parameters for circuit export as follows:

    • circuitName - name of the circuit that is being exported to Qobj

    • experimentName - name of the experiment that describes the number of memory slots, qubits, qubit names, classical bit names etc.

    • numShots - no. of trials.

  • circuitReplacement - when true exports only gates in the circuit

(Deprecated. Please use exportToQobj() instead)

To export circuit to Qobj you can also use exportQobj(circuitName, experimentName, numShots, circuitReplacement)

Example:

var qobj = circuit.exportQobj("new_circuit", false);

  • circuitName - name of the circuit that is being exported to Qobj

  • experimentName - name of the experiment that describes the number of memory slots, qubits, qubit names, classical bit names etc.

  • numShots - no. of trials.

  • circuitReplacement - when true exports only gates in the circuit

Export to python (Tensorflow Quantum)

Circuit can be exported to Tensorflow Quantum:

To export circuit to TFQ use exportToTFQ(options, exportAsGateName) method :

Example:

var tfq = circuit.exportToTFQ({comment:"Comment to insert at the beginning.\nCan be multi-line comment as this one."}, false);

  • options - consists of parameters for circuit export as follows:

    • comment - comment to insert at the beginning of the file.

    • decompose - if set to true and circuit contains user defined gates then it will be decomposed to basic gates and then exported. If set to false then user defined gates will exported as subroutines.

    • versionStr - TFQ version. Exports to latest supported version when empty string is provided. Remember - it is a string.

    • asJupyter - when this argument is true jupyter notebook will be returned.

    • shots - no. of trials.

  • exportAsGateName - name of the custom gate containing the TFQ circuit.

(Deprecated. Please use exportToTFQ() instead)

To export circuit to TFQ you can also use exportTFQ(comment, decompose, exportAsGateName, versionStr, asJupyter, shots)

Example:

var tfq = circuit.exportTFQ("Comment to insert at the beginning.\nCan be multi-line comment as this one.", false, null, null);

  • comment - comment to insert at the beginning of the file.

  • decompose - if set to true and circuit contains user defined gates then it will be decomposed to basic gates and then exported. If set to false then user defined gates will exported as subroutines.

  • exportAsGateName - name of the custom gate containing the TFQ circuit.

  • versionStr - TFQ version. Exports to latest supported version when empty string is provided. Remember - it is a string.

  • asJupyter - when this argument is true jupyter notebook will be returned.

  • shots - no. of trials.

Export to python (Braket)

Circuit can be exported to Braket:

To export circuit to Braket use exportToBraket(options, exportAsGateName) method :

Example:

var braket = circuit.exportToBraket({comment:"Comment to insert at the beginning.\nCan be multi-line comment as this one."}, false);

  • options - consists of parameters for circuit export as follows:

    • comment - comment to insert at the beginning of the file.

    • decompose - if set to true and circuit contains user defined gates then it will be decomposed to basic gates and then exported. If set to false then user defined gates will exported as subroutines.

    • versionStr - Braket version. Exports to latest supported version when empty string is provided. Remember - it is a string.

    • asJupyter - when this argument is true jupyter notebook will be returned.

    • shots - no. of trials.

    • indentDepth - The no. of tabs to be put before a Python line of code.

    • hybrid - when true exports user defined cost function along with circuit for hybrid Quantum-Classical Algorithms

  • exportAsGateName - name of the custom gate containing the Braket circuit.

(Deprecated. Please use exportToBraket() instead)

To export circuit to Braket you can also use exportBraket(comment, decompose, exportAsGateName, versionStr, asJupyter, shots, hybrid, indentDepth)

Example:

var braket = circuit.exportBraket("Comment to insert at the beginning.\nCan be multi-line comment as this one.", false, null, null);

  • comment - comment to insert at the beginning of the file.

  • decompose - if set to true and circuit contains user defined gates then it will be decomposed to basic gates and then exported. If set to false then user defined gates will exported as subroutines.

  • exportAsGateName - name of the custom gate containing the Braket circuit.

  • versionStr - Braket version. Exports to latest supported version when empty string is provided. Remember - it is a string.

  • asJupyter - when this argument is true jupyter notebook will be returned.

  • shots - no. of trials.

  • indentDepth - The no. of tabs to be put before a Python line of code.

  • hybrid - when true exports user defined cost function along with circuit for hybrid Quantum-Classical Algorithms

Export to python (pyAQASM)

Circuit can be exported to pyAQASM:

To export circuit to pyAQASM use exportToPyAQASM(options, exportAsGateName) method :

Example:

var pyAqasm = circuit.exportToPyAQASM({comment:"Comment to insert at the beginning.\nCan be multi-line comment as this one."}, false);

  • options - consists of parameters for circuit export as follows:

    • comment - comment to insert at the beginning of the file.

    • decompose - if set to true and circuit contains user defined gates then it will be decomposed to basic gates and then exported. If set to false then user defined gates will exported as subroutines.

    • asJupyter - when this argument is true jupyter notebook will be returned.

    • shots - no. of trials.

    • hybrid - when true exports user defined cost function along with circuit for hybrid Quantum-Classical Algorithms

  • exportAsGateName - name of the custom gate containing the pyAQASM circuit.

(Deprecated. Please use exportToPyAQASM() instead)

To export circuit to pyAQASM you can also use exportPyAQASM(comment, decompose, exportAsGateName, asJupyter, shots, hybrid)

Example:

var pyAqasm = circuit.exportPyAQASM("Comment to insert at the beginning.\nCan be multi-line comment as this one.", false, null, null);

  • comment - comment to insert at the beginning of the file.

  • decompose - if set to true and circuit contains user defined gates then it will be decomposed to basic gates and then exported. If set to false then user defined gates will exported as subroutines.

  • exportAsGateName - name of the custom gate containing the pyAQASM circuit.

  • asJupyter - when this argument is true jupyter notebook will be returned.

  • shots - no. of trials.

  • hybrid - when true exports user defined cost function along with circuit for hybrid Quantum-Classical Algorithms

Export to python (AQASM)

Circuit can be exported to AQASM:

To export circuit to AQASM use exportToAQASM(options, isExportPyAQASM, exportAsGateName, indentDepth) method :

Example:

var aqasm = circuit.exportToAQASM({comment:"Comment to insert at the beginning.\nCan be multi-line comment as this one."}, false);

  • options - consists of parameters for circuit export as follows:

    • comment - comment to insert at the beginning of the file.

    • decompose - if set to true and circuit contains user defined gates then it will be decomposed to basic gates and then exported. If set to false then user defined gates will exported as subroutines.

    • asJupyter - when this argument is true jupyter notebook will be returned.

    • shots - no. of trials.

    • hybrid - when true exports user defined cost function along with circuit for hybrid Quantum-Classical Algorithms

  • isExportPyAQASM - if true, this function will be used to export to pyAQASM instead of AQASM.

  • exportAsGateName - name of the custom gate containing the AQASM circuit.

  • indentDepth - The no. of tabs to be put before a Python line of code.

(Deprecated. Please use exportToAQASM() instead)

To export circuit to pyAQASM you can also use exportAQASM(comment, decompose, isExportPyAQASM, exportAsGateName, asJupyter, shots, hybrid, indentDepth)

Example:

var aqasm = circuit.exportAQASM("Comment to insert at the beginning.\nCan be multi-line comment as this one.", false, null, null);

  • comment - comment to insert at the beginning of the file.

  • decompose - if set to true and circuit contains user defined gates then it will be decomposed to basic gates and then exported. If set to false then user defined gates will exported as subroutines.

  • isExportPyAQASM - if true, this function will be used to export to pyAQASM instead of AQASM.

  • exportAsGateName - name of the custom gate containing the AQASM circuit.

  • asJupyter - when this argument is true jupyter notebook will be returned.

  • shots - no. of trials.

  • hybrid - when true exports user defined cost function along with circuit for hybrid Quantum-Classical Algorithms

  • indentDepth - The no. of tabs to be put before a Python line of code.

Export to SVG

Vector .svg image of circuit can be created with exportSVG(embedded) function with following limitations:

  • Gate symbols are non-standard. TODO (BTW, do we have standard?)

Example 1

Show circuit in browser:

// Assuming we have <div id="drawing"></div> somewhere in HTML
var container = document.getElementById("drawing");

// SVG is returned as string
var svg = circuit.exportSVG(true);

// add SVG into container
container.innerHTML = svg;

Example 2

Generate standalone SVG image at server with node.js:

// export as standalone SVG
var svg = circuit.exportSVG(false);

// do something with svg string (e.g. save to file)
...

// Or, export as embedded SVG for use in browser
svg = circuit.exportSVG(true);

// do something with svg string (e.g. serve via HTTP)
...

Export to Quirk

Circuit can be exported to popular open-source drag-and-drop quantum circuit simulator Quirk with following limitations:

  • Quirk doesn't support more than 16 qubits.

  • Quirk can possibly incorrectly interpret circuit if we have multiple controlled gates in the same column.

  • Quirk doesn't support non-sequentially positioned multi-qubit user-defined gates (for example gate on wires [3, 0, 1]) so it's best to export decomposed circuit.

Example:

var quirkData = circuit.exportQuirk(true);

var quirkURL = "http://algassert.com/quirk#circuit=" + JSON.stringify(quirkData);

// Now do something with quirkURL. Assuming this code runs in browser and we have <a id="quirk"></a> somewhere, you can:
var quirkLink = document.getElementById("quirk");
quirkLink.setAttr("href", quirkLink);

About simulator algorithm

Memory usage: up to 2 * (2^numQubits) * sizeOfComplexNumber

  • Naive implementation stores entire state vector in an array of size 2^numQubits. We are storing state in a "map", and only amplitudes with non-zero probabilities are stored. So, in worst case, size of state map is 2^n, but it's less most of the time because we don't store zeroes.

  • Naive implementation creates transformation matrix and multiplies it with state vector. We are not creating and not storing entire transformation matrix in memory. Instead, elements of transformation matrix are calculated one by one and state is multiplied and stored in new state map on the fly. This way, memory usage is minimal (in worst case we have two 2^n state vectors at a time).

  • Algorithm is parallelizable so it could use GPU, but GPU support is not implemented yet (work in progress).

Benchmark

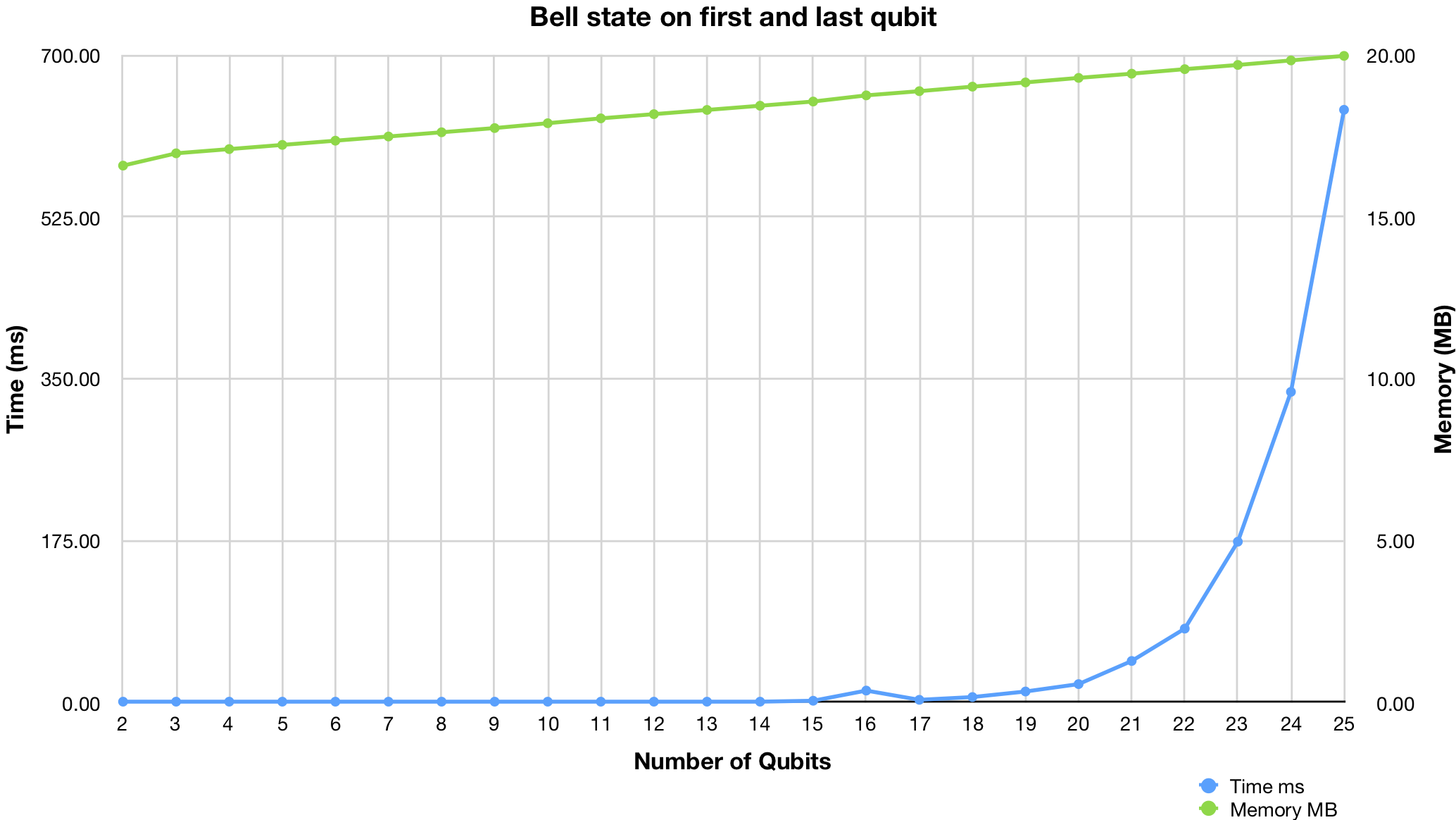
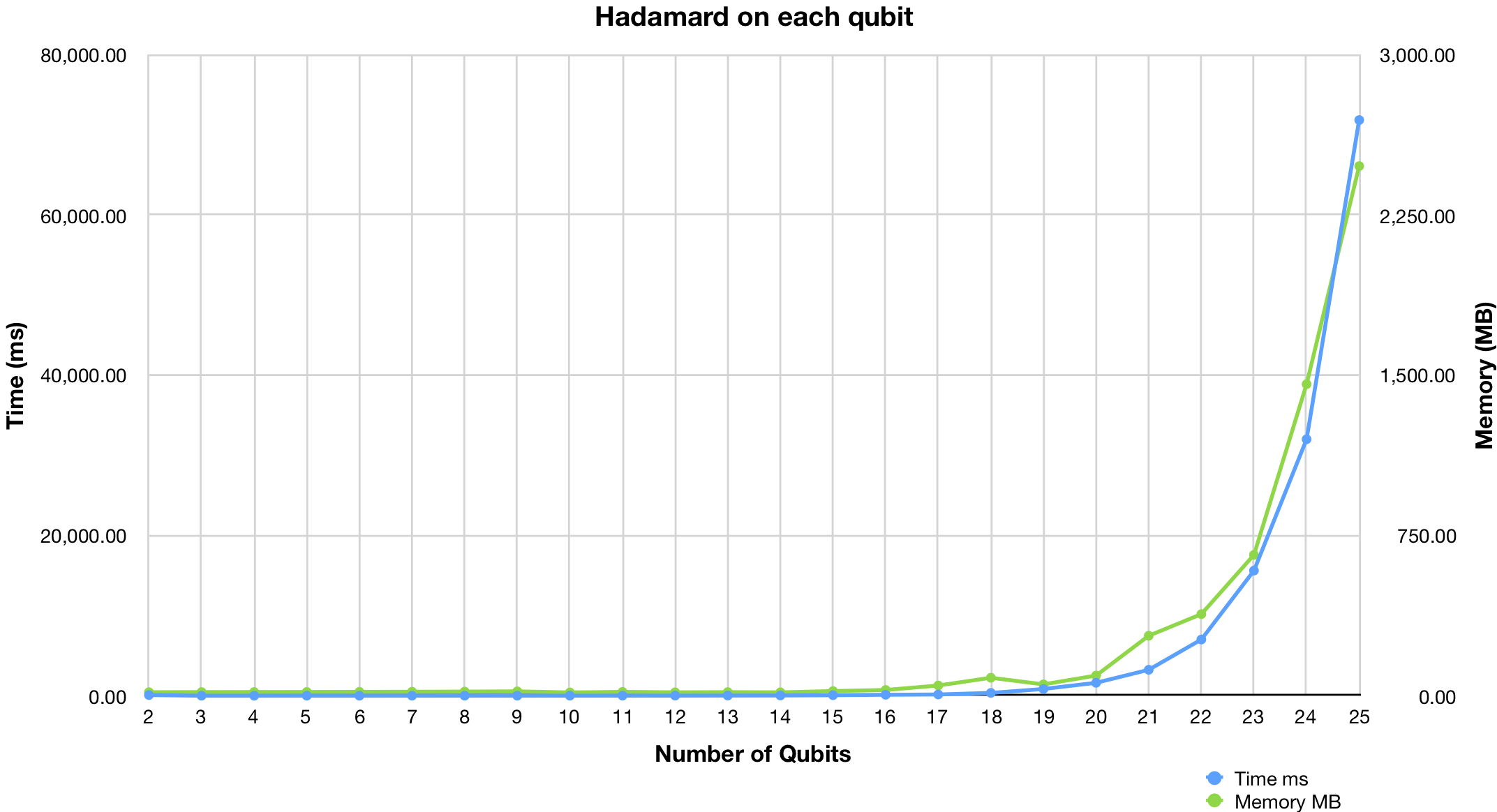
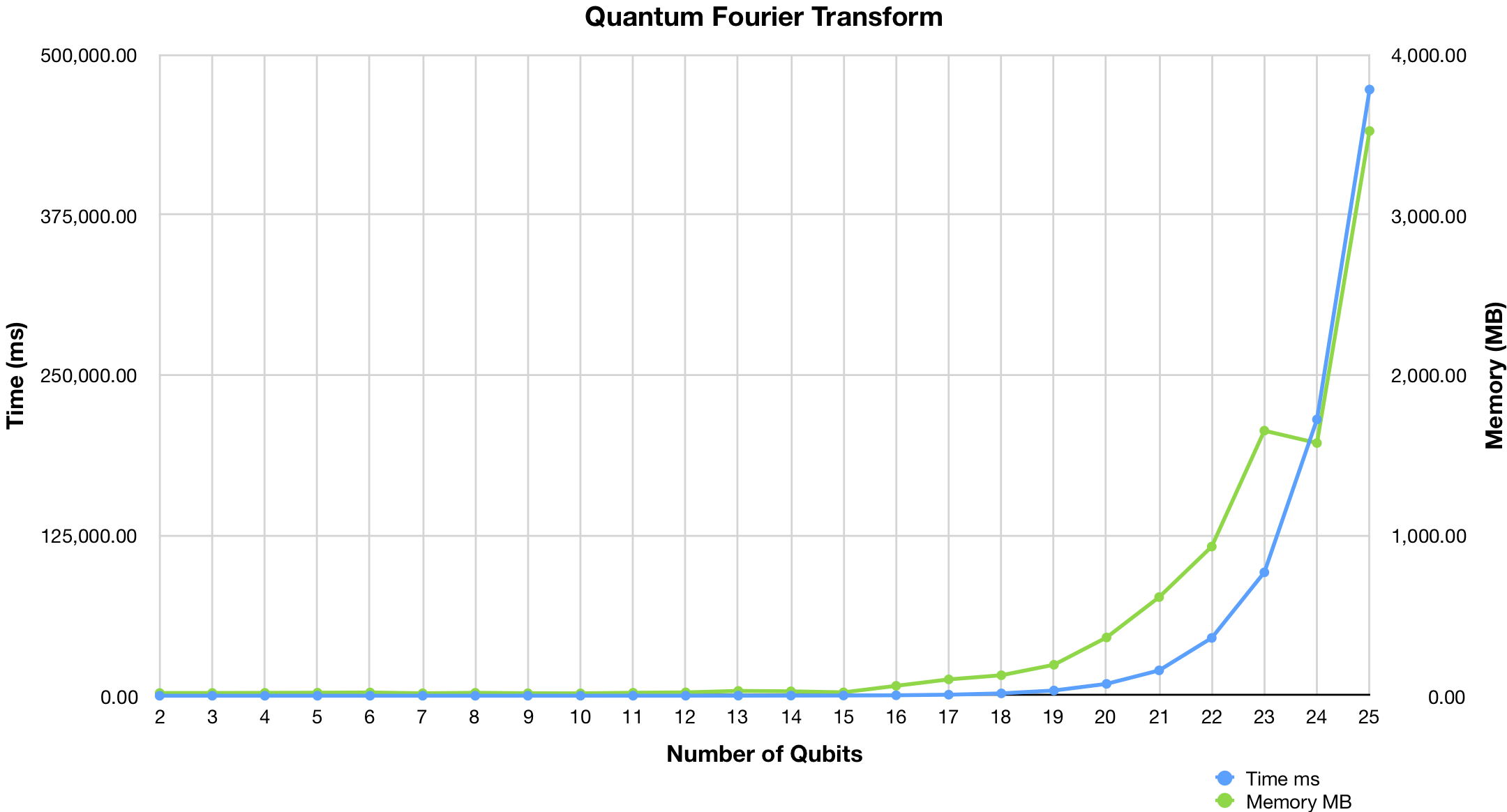
Performance is measured on MacBook Pro MJLT2 mid-2015 (Core i7 2.5 GHz, 16GB RAM)

Benchmark 1

Benchmark 2

Benchmark 3

You can find scripts in /benchmark directory.

Gates

id

Single qubit identity gate

Qubits: 1

Matrix:

[

    [1,0],
    [0,1]
]

Example:

circuit.appendGate("id", 0);

x

Pauli X (PI rotation over X-axis) aka "NOT" gate

Qubits: 1

Matrix:

[

    [0,1],
    [1,0]
]

Example:

circuit.appendGate("x", 0);

y

Pauli Y (PI rotation over Y-axis)

Qubits: 1

Matrix:

[

    [0,"-i"],
    ["i",0]
]

Example:

circuit.appendGate("y", 0);

z

Pauli Z (PI rotation over Z-axis)

Qubits: 1

Matrix:

[

    [1,0],
    [0,-1]
]

Example:

circuit.appendGate("z", 0);

h

Hadamard gate

Qubits: 1

Matrix:

[

    ["1 / sqrt(2)","1 / sqrt(2)"],
    ["1 / sqrt(2)","-1 / sqrt(2)"]
]

Example:

circuit.appendGate("h", 0);

srn

Square root of NOT

Qubits: 1

Matrix:

[

    ["0.5+0.5i","0.5-0.5i"],
    ["0.5-0.5i","0.5+0.5i"]
]

Example:

circuit.appendGate("srn", 0);

srndg

Inverse square root of NOT

Qubits: 1

Matrix:

[

    ["0.5-0.5i","0.5+0.5i"],
    ["0.5+0.5i","0.5-0.5i"]
]

Example:

circuit.appendGate("srndg", 0);

r2

PI/2 rotation over Z-axis aka "Phase PI/2"

Qubits: 1

Matrix:

[

    [1,0],
    [0,"exp(i * pi / 2)"]
]

Example:

circuit.appendGate("r2", 0);

r4

PI/4 rotation over Z-axis aka "Phase PI/4"

Qubits: 1

Matrix:

[

    [1,0],
    [0,"exp(i * pi / 4)"]
]

Example:

circuit.appendGate("r4", 0);

r8

PI/8 rotation over Z-axis aka "Phase PI/8"

Qubits: 1

Matrix:

[

    [1,0],
    [0,"exp(i * pi / 8)"]
]

Example:

circuit.appendGate("r8", 0);

rx

Rotation around the X-axis by given angle

Qubits: 1

Parameters:

  • theta

Matrix:

[

    ["cos(theta / 2)","-i * sin(theta / 2)"],
    ["-i * sin(theta / 2)","cos(theta / 2)"]
]

Example:

circuit.appendGate("rx", 0, {
    params: {
        theta: "pi/2"
    }
});

ry

Rotation around the Y-axis by given angle

Qubits: 1

Parameters:

  • theta

Matrix:

[

    ["cos(theta / 2)","-1 * sin(theta / 2)"],
    ["sin(theta / 2)","cos(theta / 2)"]
]

Example:

circuit.appendGate("ry", 0, {
    params: {
        theta: "pi/2"
    }
});

rz

Rotation around the Z-axis by given angle

Qubits: 1

Parameters:

  • phi

Matrix:

[

    ["cos(phi / 2) - i * sin(phi / 2)",0],
    [0,"cos(phi / 2) + i * sin(phi / 2)"]
]

Example:

circuit.appendGate("rz", 0, {
    params: {
        phi: "pi/2"
    }
});

u1

Single-qubit rotation about the Z axis

Qubits: 1

Parameters:

  • lambda

Matrix:

[

    [1,0],
    [0,"exp(i * lambda)"]
]

Example:

circuit.appendGate("u1", 0, {
    params: {
        lambda: "pi/2"
    }
});

u2

Single-qubit rotation about the X+Z axis

Qubits: 1

Parameters:

  • phi
  • lambda

Matrix:

[

    ["1 / sqrt(2)","-exp(i * lambda) * 1 / sqrt(2)"],
    ["exp(i * phi) * 1 / sqrt(2)","exp(i * lambda + i * phi) * 1 / sqrt(2)"]
]

Example:

circuit.appendGate("u2", 0, {
    params: {
        phi: "pi/2",
        lambda: "pi/2"
    }
});

u3

Generic single-qubit rotation gate with 3 Euler angles

Qubits: 1

Parameters:

  • theta
  • phi
  • lambda

Matrix:

[

    ["cos(theta/2)","-exp(i * lambda) * sin(theta / 2)"],
    ["exp(i * phi) * sin(theta / 2)","exp(i * lambda + i * phi) * cos(theta / 2)"]
]

Example:

circuit.appendGate("u3", 0, {
    params: {
        theta: "pi/2",
        phi: "pi/2",
        lambda: "pi/2"
    }
});

s

PI/2 rotation over Z-axis (synonym for r2)

Qubits: 1

Matrix:

[

    [1,0],
    [0,"exp(i * pi / 2)"]
]

Example:

circuit.appendGate("s", 0);

t

PI/4 rotation over Z-axis (synonym for r4)

Qubits: 1

Matrix:

[

    [1,0],
    [0,"exp(i * pi / 4)"]
]

Example:

circuit.appendGate("t", 0);

sdg

(-PI/2) rotation over Z-axis

Qubits: 1

Matrix:

[

    [1,0],
    [0,"exp(-i * pi / 2)"]
]

Example:

circuit.appendGate("sdg", 0);

tdg

(-PI/4) rotation over Z-axis

Qubits: 1

Matrix:

[

    [1,0],
    [0,"exp(-i * pi / 4)"]
]

Example:

circuit.appendGate("tdg", 0);

gpi

GPi gate

Qubits: 1

Parameters:

  • phi

Matrix:

[

    [0,"exp(-i*phi)"],
    ["exp(i*phi)",0]
]

Example:

circuit.appendGate("gpi", 0, {
    params: {
        phi: "pi/2"
    }
});

gpi2

GPi2 gate

Qubits: 1

Parameters:

  • phi

Matrix:

[

    ["1/sqrt(2)","(-i*exp(-i*phi))/sqrt(2)"],
    ["(-i*exp(i*phi))/sqrt(2)","1/sqrt(2)"]
]

Example:

circuit.appendGate("gpi2", 0, {
    params: {
        phi: "pi/2"
    }
});

vz

VirtualZ gate

Qubits: 1

Parameters:

  • theta

Matrix:

[

    ["exp(-i*theta/2)",0],
    [0,"exp(i*theta/2)"]
]

Example:

circuit.appendGate("vz", 0, {
    params: {
        theta: "pi/2"
    }
});

cx

Controlled NOT (CNOT) gate

Qubits: 2

Matrix:

[

    [1,0,0,0],
    [0,1,0,0],
    [0,0,0,1],
    [0,0,1,0]
]

Example:

circuit.appendGate("cx", [0, 1]);

cy

Controlled Y gate (controlled rotation over Y-axis by PI)

Qubits: 2

Matrix:

[

    [1,0,0,0],
    [0,1,0,0],
    [0,0,0,"-i"],
    [0,0,"i",0]
]

Example:

circuit.appendGate("cy", [0, 1]);

cz

Controlled Z gate (controlled rotation over Z-axis by PI)

Qubits: 2

Matrix:

[

    [1,0,0,0],
    [0,1,0,0],
    [0,0,1,0],
    [0,0,0,-1]
]

Example:

circuit.appendGate("cz", [0, 1]);

ch

Controlled Hadamard gate

Qubits: 2

Matrix:

[

    [1,0,0,0],
    [0,1,0,0],
    [0,0,"1 / sqrt(2)","1 / sqrt(2)"],
    [0,0,"1 / sqrt(2)","-1 / sqrt(2)"]
]

Example:

circuit.appendGate("ch", [0, 1]);

csrn

Controlled square root of NOT

Qubits: 2

Matrix:

[

    [1,0,0,0],
    [0,1,0,0],
    [0,0,"0.5+0.5i","0.5-0.5i"],
    [0,0,"0.5-0.5i","0.5+0.5i"]
]

Example:

circuit.appendGate("csrn", [0, 1]);

swap

Swaps the state of two qubits.

Qubits: 2

Matrix:

[

    [1,0,0,0],
    [0,0,1,0],
    [0,1,0,0],
    [0,0,0,1]
]

Example:

circuit.appendGate("swap", [0, 1]);

srswap

Square root of swap

Qubits: 2

Matrix:

[

    [1,0,0,0],
    [0,"0.5 * (1 + i)","0.5 * (1 - i)",0],
    [0,"0.5 * (1 - i)","0.5 * (1 + i)",0],
    [0,0,0,1]
]

Example:

circuit.appendGate("srswap", [0, 1]);

iswap

Swaps the state of two qubits, applying a -i phase to q1 when it is in the 1 state and a -i phase to q2 when it is in the 0 state

Qubits: 2

Matrix:

[

    [1,0,0,0],
    [0,0,"0+i",0],
    [0,"0+i",0,0],
    [0,0,0,1]
]

Example:

circuit.appendGate("iswap", [0, 1]);

xx

XX gate

Qubits: 2

Parameters:

  • theta

Matrix:

[

    ["cos(theta)",0,0,"-i*sin(theta)"],
    [0,"cos(theta)","-i*sin(theta)",0],
    [0,"-i*sin(theta)","cos(theta)",0],
    ["-i*sin(theta)",0,0,"cos(theta)"]
]

Example:

circuit.appendGate("xx", [0, 1], {
    params: {
        theta: "pi/2"
    }
});

yy

YY gate

Qubits: 2

Parameters:

  • theta

Matrix:

[

    ["cos(theta)",0,0,"i*sin(theta)"],
    [0,"cos(theta)","-i*sin(theta)",0],
    [0,"-i*sin(theta)","cos(theta)",0],
    ["i*sin(theta)",0,0,"cos(theta)"]
]

Example:

circuit.appendGate("yy", [0, 1], {
    params: {
        theta: "pi/2"
    }
});

zz

Parametric 2-qubit rotation about ZZ

Qubits: 2

Parameters:

  • theta

Matrix:

[

    ["exp(-i * theta / 2)",0,0,0],
    [0,"exp(i * theta / 2)",0,0],
    [0,0,"exp(i * theta / 2)",0],
    [0,0,0,"exp(-i * theta / 2)"]
]

Example:

circuit.appendGate("zz", [0, 1], {
    params: {
        theta: "pi/2"
    }
});

xy

XY gate

Qubits: 2

Parameters:

  • phi

Matrix:

[

    [1,0,0,0],
    [0,"cos(phi / 2)","i * sin(phi / 2)",0],
    [0,"i * sin(phi / 2)","cos(phi / 2)",0],
    [0,0,0,1]
]

Example:

circuit.appendGate("xy", [0, 1], {
    params: {
        phi: "pi/2"
    }
});

ms

Mølmer-Sørensen gate

Qubits: 2

Parameters:

  • phi0
  • phi1

Matrix:

[

    ["1/sqrt(2)",0,0,"(-i*exp(-i*(phi0+phi1)))/sqrt(2)"],
    [0,"1/sqrt(2)","(-i*exp(-i*(phi0-phi1)))/sqrt(2)",0],
    [0,"(-i*exp(i*(phi0-phi1)))/sqrt(2)","1/sqrt(2)",0],
    ["(-i*exp(i*(phi0+phi1)))/sqrt(2)",0,0,"1/sqrt(2)"]
]

Example:

circuit.appendGate("ms", [0, 1], {
    params: {
        phi0: "pi/2",
        phi1: "pi/2"
    }
});

cr2

Controlled PI/2 rotation over Z-axis

Qubits: 2

Matrix:

[

    [1,0,0,0],
    [0,1,0,0],
    [0,0,1,0],
    [0,0,0,"exp(i * pi / 2)"]
]

Example:

circuit.appendGate("cr2", [0, 1]);

cr4

Controlled PI/4 rotation over Z-axis

Qubits: 2

Matrix:

[

    [1,0,0,0],
    [0,1,0,0],
    [0,0,1,0],
    [0,0,0,"exp(i * pi / 4)"]
]

Example:

circuit.appendGate("cr4", [0, 1]);

cr8

Controlled PI/8 rotation over Z-axis

Qubits: 2

Matrix:

[

    [1,0,0,0],
    [0,1,0,0],
    [0,0,1,0],
    [0,0,0,"exp(i * pi / 8)"]
]

Example:

circuit.appendGate("cr8", [0, 1]);

crx

Controlled rotation around the X-axis by given angle

Qubits: 2

Parameters:

  • theta

Matrix:

[

    [1,0,0,0],
    [0,1,0,0],
    [0,0,"cos(theta / 2)","-i * sin(theta / 2)"],
    [0,0,"-i * sin(theta / 2)","cos(theta / 2)"]
]

Example:

circuit.appendGate("crx", [0, 1], {
    params: {
        theta: "pi/2"
    }
});

cry

Controlled rotation around the Y-axis by given angle

Qubits: 2

Parameters:

  • theta

Matrix:

[

    [1,0,0,0],
    [0,1,0,0],
    [0,0,"cos(theta / 2)","-1 * sin(theta / 2)"],
    [0,0,"sin(theta / 2)","cos(theta / 2)"]
]

Example:

circuit.appendGate("cry", [0, 1], {
    params: {
        theta: "pi/2"
    }
});

crz

Controlled rotation around the Z-axis by given angle

Qubits: 2

Parameters:

  • phi

Matrix:

[

    [1,0,0,0],
    [0,1,0,0],
    [0,0,"cos(phi / 2) - i * sin(phi / 2)",0],
    [0,0,0,"cos(phi / 2) + i * sin(phi / 2)"]
]

Example:

circuit.appendGate("crz", [0, 1], {
    params: {
        phi: "pi/2"
    }
});

cu1

Controlled rotation about the Z axis

Qubits: 2

Parameters:

  • lambda

Matrix:

[

    [1,0,0,0],
    [0,1,0,0],
    [0,0,1,0],
    [0,0,0,"exp(i * lambda)"]
]

Example:

circuit.appendGate("cu1", [0, 1], {
    params: {
        lambda: "pi/2"
    }
});

cu2

Controlled rotation about the X+Z axis

Qubits: 2

Parameters:

  • phi
  • lambda

Matrix:

[

    [1,0,0,0],
    [0,1,0,0],
    [0,0,"1 / sqrt(2)","-exp(i * lambda) * 1 / sqrt(2)"],
    [0,0,"exp(i * phi) * 1 / sqrt(2)","exp(i * lambda + i * phi) * 1 / sqrt(2)"]
]

Example:

circuit.appendGate("cu2", [0, 1], {
    params: {
        phi: "pi/2",
        lambda: "pi/2"
    }
});

cu3

Controlled rotation gate with 3 Euler angles

Qubits: 2

Parameters:

  • theta
  • phi
  • lambda

Matrix:

[

    [1,0,0,0],
    [0,1,0,0],
    [0,0,"cos(theta/2)","-exp(i * lambda) * sin(theta / 2)"],
    [0,0,"exp(i * phi) * sin(theta / 2)","exp(i * lambda + i * phi) * cos(theta / 2)"]
]

Example:

circuit.appendGate("cu3", [0, 1], {
    params: {
        theta: "pi/2",
        phi: "pi/2",
        lambda: "pi/2"
    }
});

cs

Controlled PI/2 rotation over Z-axis (synonym for cr2)

Qubits: 2

Matrix:

[

    [1,0,0,0],
    [0,1,0,0],
    [0,0,1,0],
    [0,0,0,"exp(i * pi / 2)"]
]

Example:

circuit.appendGate("cs", [0, 1]);

ct

Controlled PI/4 rotation over Z-axis (synonym for cr4)

Qubits: 2

Matrix:

[

    [1,0,0,0],
    [0,1,0,0],
    [0,0,1,0],
    [0,0,0,"exp(i * pi / 4)"]
]

Example:

circuit.appendGate("ct", [0, 1]);

csdg

Controlled (-PI/2) rotation over Z-axis

Qubits: 2

Matrix:

[

    [1,0,0,0],
    [0,1,0,0],
    [0,0,1,0],
    [0,0,0,"exp(-i * pi / 2)"]
]

Example:

circuit.appendGate("csdg", [0, 1]);

ctdg

Controlled (-PI/4) rotation over Z-axis

Qubits: 2

Matrix:

[

    [1,0,0,0],
    [0,1,0,0],
    [0,0,1,0],
    [0,0,0,"exp(-i * pi / 4)"]
]

Example:

circuit.appendGate("ctdg", [0, 1]);

ccx

Toffoli aka "CCNOT" gate

Qubits: 3

Matrix:

[

    [1,0,0,0,0,0,0,0],
    [0,1,0,0,0,0,0,0],
    [0,0,1,0,0,0,0,0],
    [0,0,0,1,0,0,0,0],
    [0,0,0,0,1,0,0,0],
    [0,0,0,0,0,1,0,0],
    [0,0,0,0,0,0,0,1],
    [0,0,0,0,0,0,1,0]
]

Example:

circuit.appendGate("ccx", [0, 1, 2]);

cswap

Controlled swap aka "Fredkin" gate

Qubits: 3

Matrix:

[

    [1,0,0,0,0,0,0,0],
    [0,1,0,0,0,0,0,0],
    [0,0,1,0,0,0,0,0],
    [0,0,0,1,0,0,0,0],
    [0,0,0,0,1,0,0,0],
    [0,0,0,0,0,0,1,0],
    [0,0,0,0,0,1,0,0],
    [0,0,0,0,0,0,0,1]
]

Example:

circuit.appendGate("cswap", [0, 1, 2]);

csrswap

Controlled square root of swap

Qubits: 3

Matrix:

[

    [1,0,0,0,0,0,0,0],
    [0,1,0,0,0,0,0,0],
    [0,0,1,0,0,0,0,0],
    [0,0,0,1,0,0,0,0],
    [0,0,0,0,1,0,0,0],
    [0,0,0,0,0,"0.5 * (1 + i)","0.5 * (1 - i)",0],
    [0,0,0,0,0,"0.5 * (1 - i)","0.5 * (1 + i)",0],
    [0,0,0,0,0,0,0,1]
]

Example:

circuit.appendGate("csrswap", [0, 1, 2]);

reset

Resets qubit

Qubits: 1

Example:

circuit.appendGate("reset", 0);

measure

Measures qubit and stores chance (0 or 1) into classical bit

Qubits: 1

Example:

circuit.appendGate("measure", 0, {
    creg: {
        name: "c",
        bit: 3
    }
});

Or:

circuit.addMeasure(0, "c", 3);

API docs

To be written...

License

MIT

Readme

Keywords

Package Sidebar

Install

npm i quantum-circuit

Repository

github.com/quantastica/quantum-circuit

Homepage

quantum-circuit.com

Weekly Downloads

458

Version

0.9.222

License

MIT

Unpacked Size

14.2 MB

Total Files

47

Last publish

Collaborators

  • perak
Try on RunKit
Report malware