scijs-window-functions
Window functions for digital signal processing
Introduction
Among other uses, window functions help control spectral leakage when doing Fourier Analysis. This collection of window functions is copied directly from Wikipedia. Caveat emptor.
Usage
To require all window functions, include the top-level scijs-window-functions module:
var wfuncs = var value = wfuncsYou can also require a single window function:
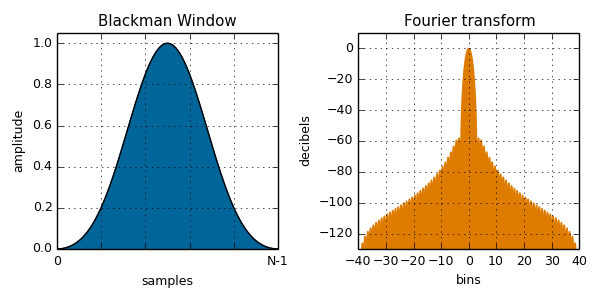
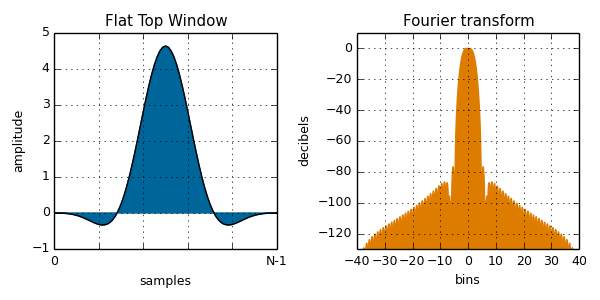
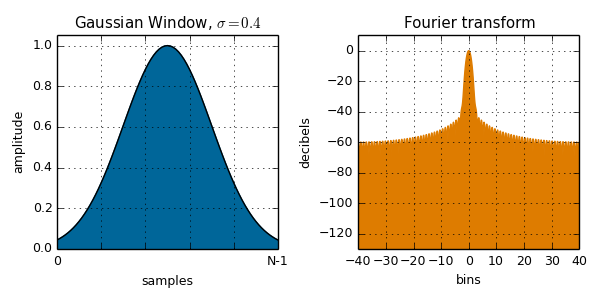
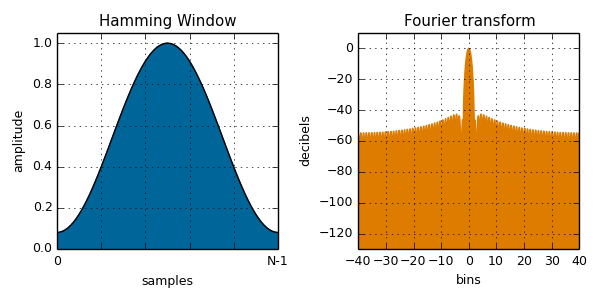
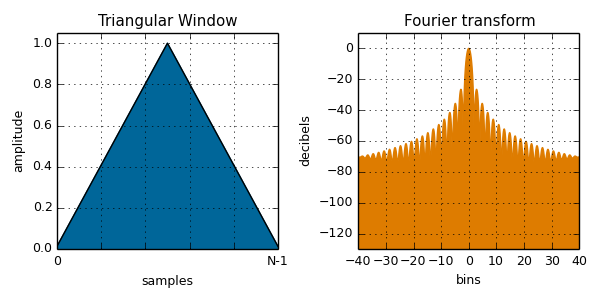
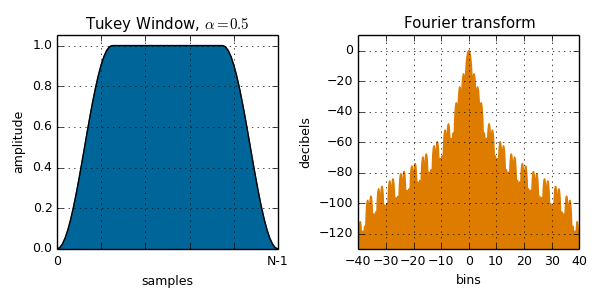
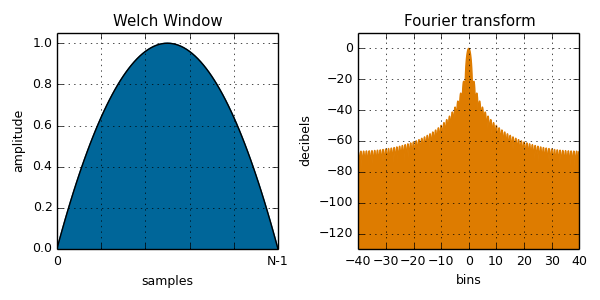
var blackmanHarris = var value = To calculate the value of a window function, pass the sample number and total number of samples to one of the window functions listed below, along with any additional parameters it may require. The plots below are calculated from the npm module and plotted with Fourier transform to illustrate the spectral leakage. See the Wikipedia page on window functions for more details.
- Bartlett-Hann
- Bartlett
- Blackman-Harris
- Blackman-Nuttall
- Cosine
- Exact Blackman
- Flat top
- Gaussian
- Hamming
- Hann
- Lanczos
- Nuttall
- Rectangular
- Triangular
- Tukey
- Welch
bartlettHann( i, N ):
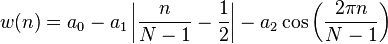
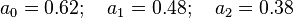
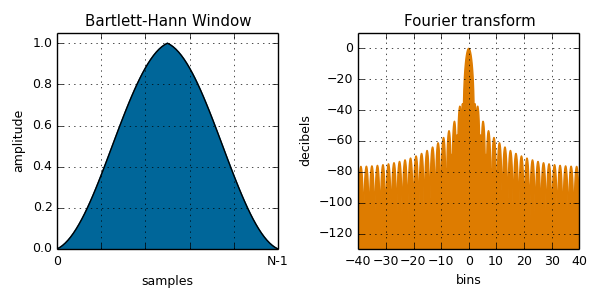
bartlett( i, N ):
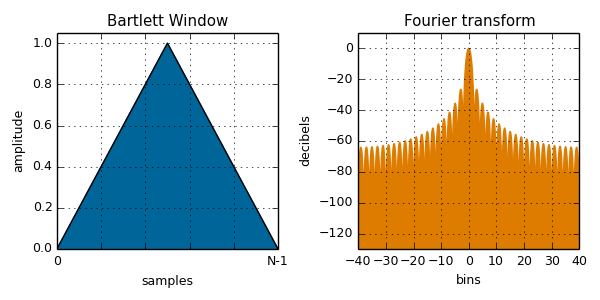
blackman( i, N ):
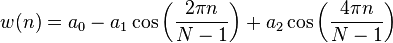
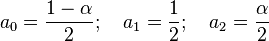
blackmanHarris( i, N ):
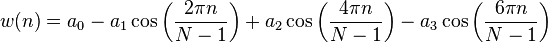

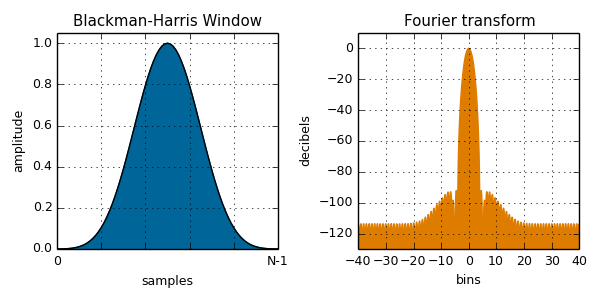
blackmanNuttall( i, N ):
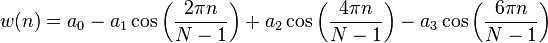

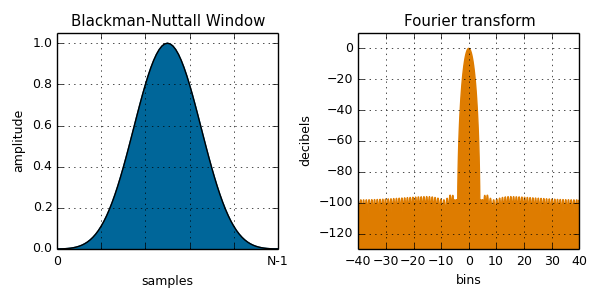
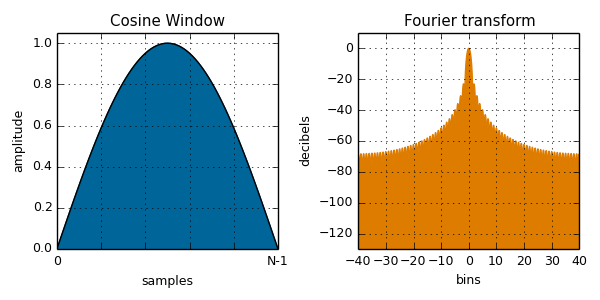
cosine( i, N ):
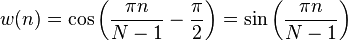
exactBlackman( i, N ):
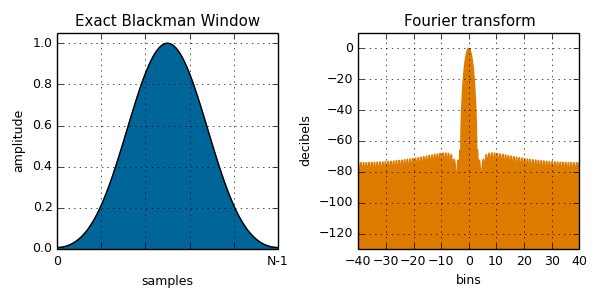
The same as the Blackman window, except a0 = 0.42659 a1 = 0.49656, and a2 = 0.076849. These place zeros at the third and fourth sidelobes.
flatTop( i, N ):
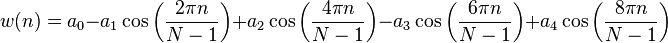
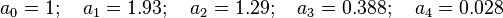
gaussian( i, N, sigma ):
Sigma controls the width of the window.
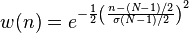
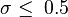
hamming( i, N ):
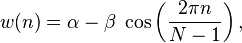
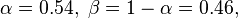
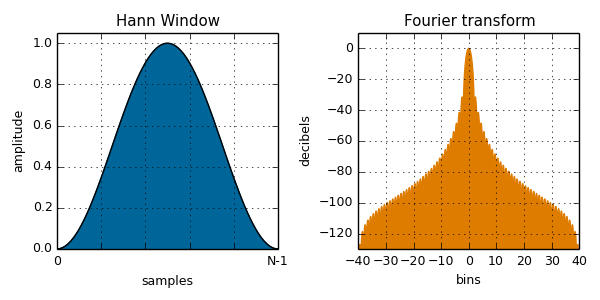
hann( i, N ):
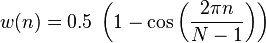
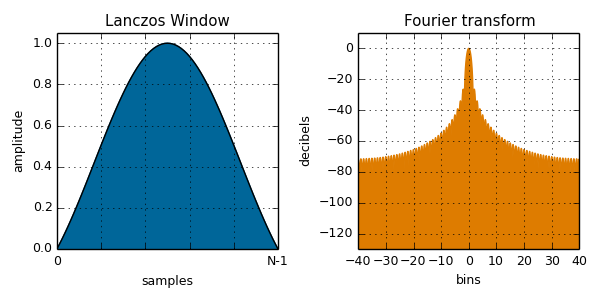
lanczos( i, N ):
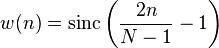
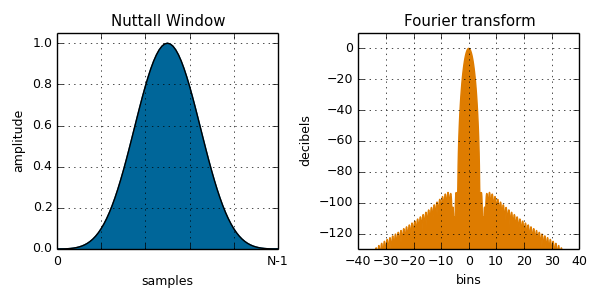
nuttall( i, N ):
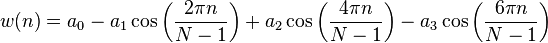

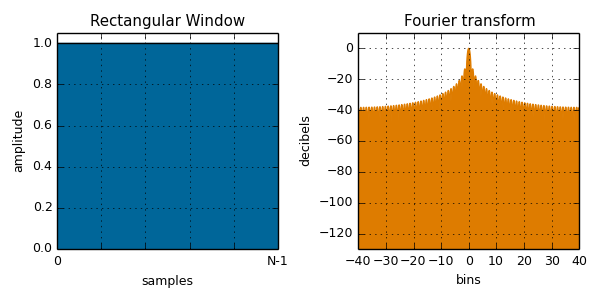
rectangular( i, N ):
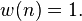
triangular( i, N ):
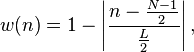
tukey( i, N, alpha ):
A tapered cosine window. Alpha controls the relative width of the flat section. Alpha=0 is rectangular, alpha=1 is Hann. 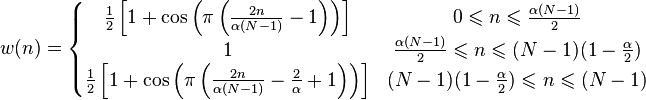
welch( i, N ):
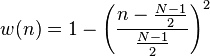
Testing
The tests ensure the window functions aren't returning NaN, but it's hard to have confidence in the accuracy with tests. Instead, I opted to focus on visual testing via plots and Fourier Transforms. To generate the plots, run
$ npm run generate-plotsIt pipes them through matplotlib. Don't worry. I realize the irony.
Credits
Window function definitions and equation images from Wikipedia: Window Function.
(c) 2015 Ricky Reusser. MIT License