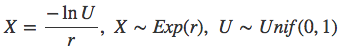poisson-process.js
A JavaScript library to generate naturally varying time intervals. It improves realism and natural unpredictability in your games or animations like aliens walking by a window, or cars trying to drive over your character on a busy road. It removes bottlenecks in distributed systems by adding jitter that prevents thundering herd problem. It can also simulate the frequency of chat messages, page loads or arriving emails as well as queues, traffic and earthquakes. The underlying mathematical concept is called the Poisson process.
In the animation above, the blue cars drive by in constant time intervals and the red ones in more natural, randomized intervals typical for the Poisson process.
Examples – Installation – Usage – API – Theory – Contribute
Examples
- Poisson's Stroboscope
- Sprinkler.js depends on poisson-process.js. Look for the examples section.
Installation
Node.js & CommonJS
First $ npm install poisson-process and then:
var poissonProcess = require('poisson-process');
Browsers
First download poisson-process.min.js and then:
<script src="poisson-process.min.js"></script>
Require.js & Async Module Definition AMD
First download poisson-process.min.js and then:
define(['scripts/poisson-process'], function (poissonProcess) { ... });
Usage
It is simple; you specify an average call interval in milliseconds, a function to be called and then start the process.
> var p = poissonProcess.create(500, function message() {
console.log('A message arrived.')
})
> p.start()
Now the message function will be called each 500 milliseconds in average. The delay from a previous call can vary from near 0 milliseconds to a time that is significantly longer than the given average, even though the extremes are increasingly unlikely.
The process is paused by:
> p.stop()
If you desire just numbers, generate intervals by:
> poissonProcess.sample(500)
389.33242512
> poissonProcess.sample(500)
506.58621391
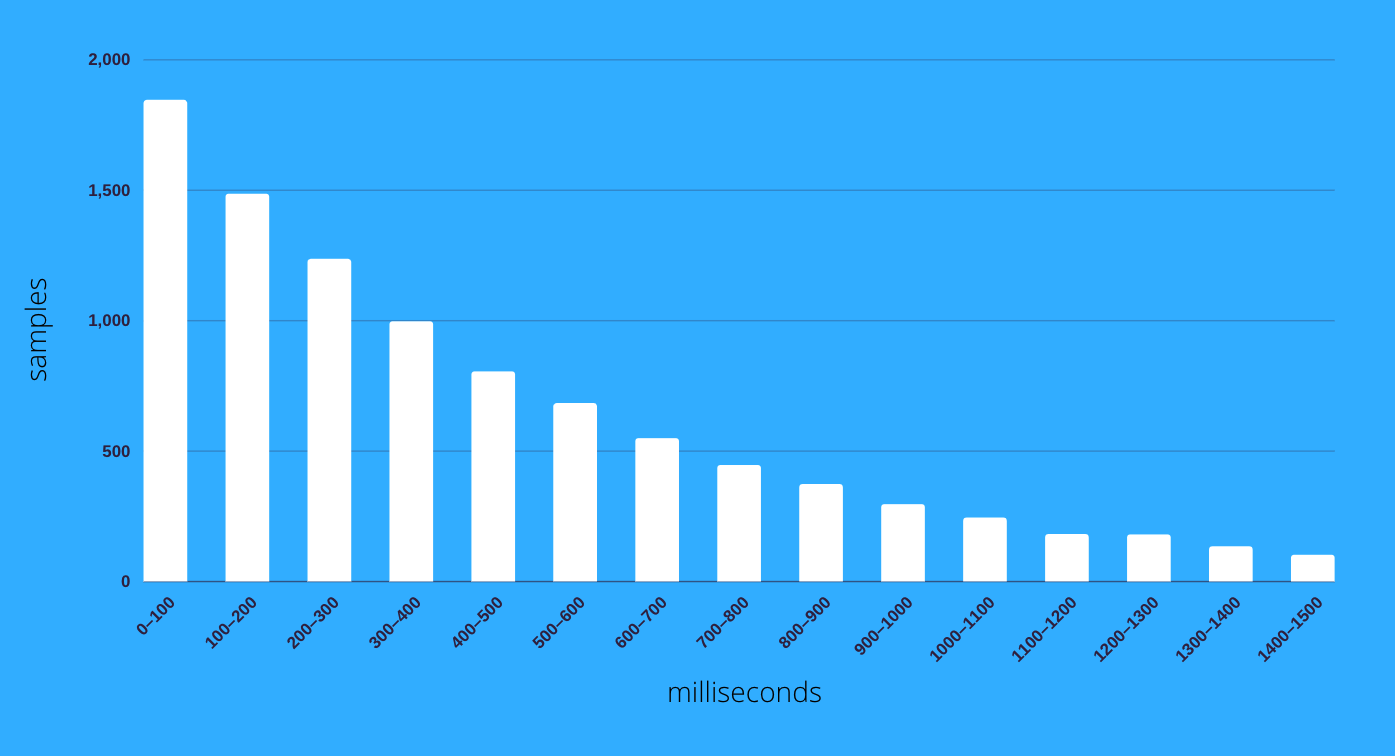
The chart below displays distribution of 10000 samples taken with the average interval of 500 milliseconds. The samples are grouped in 100 ms bins and the samples above 1500 ms are not charted. While 18 % of the samples are below 100 ms, the long tail of the large intervals balances the distribution at the average of 500 ms.
Chart: Shape of the distribution. 10000 samples grouped in 100 ms wide bins.
API
poissonProcess.create(averageIntervalMs, triggerFunction)
The create constructor takes in two parameters. The averageIntervalMs is an integer and the average interval in milliseconds to call the triggerFunction. The triggerFunction takes no parameters and does not have to return anything.
var p = poissonProcess.create(500, function message() {
console.log('A message arrived.')
})
p.start()
Start the process; begin to call the triggerFunction.
p.start()
p.stop()
Stop the process; do not anymore call the triggerFunction.
p.stop()
poissonProcess.sample(average)
The sample generates time intervals of Poisson distributed events. It returns a number; a sample from the exponential distribution with the rate 1 / average.
Note the difference between Poisson distribution and its interval distribution. Where a sample of Poisson distribution would represent a number of events happening within a fixed time window, its interval distribution represents the time between the events. The sample method implements the latter.
> poissonProcess.sample(500)
323.02...
> poissonProcess.sample(500)
returns 941.33...
> poissonProcess.sample(500)
returns 609.86...
Theory
The poisson-process.js is based on the mathematical concept of the Poisson process. It is a stochastic process that is usually perceived in the frequency of earthquakes, arriving mail and, in general, the other series of events where a single event, like an arriving letter, does not much depend on the other events, like the preceding or following letters.
It is known that inter-arrival times of the events in a Poisson process follow an exponential probability distribution with a rate parameter r. It is also known that the multiplicative inverse of r, 1/r is the mean of the inter-arrival times. Therefore to generate an event each m milliseconds in average, we sample the exponential distribution of the rate 1/m. Sampling the exponential distribution is rather simple as it follows the rule:
In our test suite, we proof by simulation that our sampling method forms an exponential distribution with correct mean and variance. The variance of an exponential distribution is known to be 1/(r*r). We also proof that this leads to a Poisson distributed behavior. Run the test suite by first $ npm install and then $ npm test.
A detailed and enjoyable introduction to the theory is given by Jeff Preshing at How to Generate Random Timings for a Poisson Process. Wikipedia's article Poisson point process also provides a comprehensive introduction and a set of references.
Contribute
Issues and pull request are warmly welcome. Run tests with $ npm test before submitting.
Build bundle and source maps with $ npm run build.