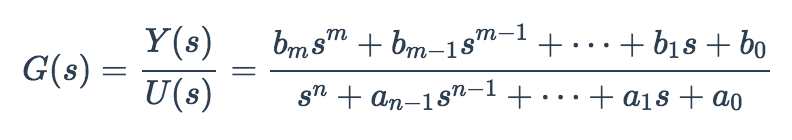ndarray-tf2ss
Converts a transfer function representation to state space.
Usage
The transfer function is defined using the following notation:
With that convention, some pseudocode for usage would be:
y = [bm, ... , b1, b0];
x = [1, an-1, ..., a1, a0];
[A, B, C, D] = require('ndarray-tf2ss')(y, x);
The y and x arguments need to be ndarrays. Each row in the input arguments defines a separate function to be calculated. Single input-single output (SISO) systems can be defined with y having a single row and x having a single row.
Description
A transfer function typically relates the input of a system to an output. Control systems may need a state-space representation, and this function can convert the transfer function to the necessary matrices, which will be ndarrays.
State-space control needs 4 matrices and they satisfy the equations:
dx = Ax + Bu
y = Cx + Du
where dx is the derivative of the state variables. Note that the D matrix is zero. If m < n, the D matrix will always be zero. For causality (i.e. that we don't have to take into account future inputs), m ≤ n.
Author
Tim Bright
License
© 2016, Tim Bright. MIT License.