modified-newton-raphson
Find zeros of a function using the Modified Newton-Raphson method
Introduction
The Newton-Raphson method uses the tangent of a curve to iteratively approximate a zero of a function, f(x). The Modified Newton-Raphson [1][2] method uses the fact that f(x) and u(x) := f(x)/f'(x) have the same zeros and instead approximates a zero of u(x). That is, by defining
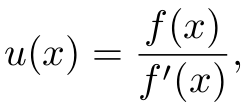
u(x),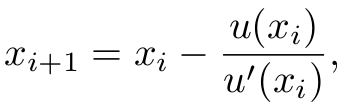
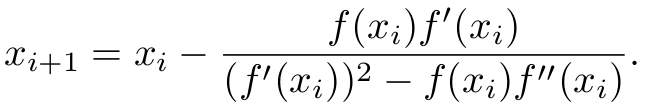
In other words, by effectively estimating the order of convergence, it overrelaxes or underrelaxes the update, in particular converging much more quickly for roots with multiplicity greater than 1.
Example
Consider the zero of (x + 2) * (x - 1)^4 at x = 1. Due to its multiplicity, Newton-Raphson is likely to reach the maximum number of iterations before converging. Modified Newton-Raphson computes the multiplicity and overrelaxes, converging quickly using either provided derivatives or numerical differentiation.
var mnr = ; { return Math * x + 2; } { return 4 * Math * x + 2 + Math; } { return 12 * Math * x + 2 + 8 * Math; } // Using first and second derivatives:// => 1.0000000000000000 (4 iterations) // Using numerical second derivative:// => 1.000000000003979 (4 iterations) // Using numerical first and second derivatives:// => 0.9999999902458561 (4 iterations)Installation
$ npm install modified-newton-raphsonAPI
require('modified-newton-raphson')(f[, fp[, fpp]], x0[, options])
Given a real-valued function of one variable, iteratively improves and returns a guess of a zero.
Parameters:
f: The numerical function of one variable of which to compute the zero.fp(optional): The first derivative off. If not provided, is computed numerically using a fourth order central difference with step sizeh.fpp(optional): The second derivative off. If bothfpandfppare not provided, is computed numerically using a fourth order central difference with step sizeh. Iffpis provided andfppis not, then is computed using a fourth order first central difference offp.x0: A number representing the intial guess of the zero.options(optional): An object permitting the following options:tolerance(default:1e-7): The tolerance by which convergence is measured. Convergence is met if|x[n+1] - x[n]| <= tolerance * |x[n+1]|.epsilon(default:2.220446049250313e-16(double-precision epsilon)): A threshold against which the first derivative is tested. Algorithm fails if|y'| < epsilon * |y|.maxIter(default:20): Maximum permitted iterations.h(default:1e-4): Step size for numerical differentiation.verbose(default:false): Output additional information about guesses, convergence, and failure.
Returns: If convergence is achieved, returns an approximation of the zero. If the algorithm fails, returns false.
See Also
References
[1] Wu, X., Roots of Equations, Course notes.
[2] Mathews, J., The Accelerated and Modified Newton Methods, Course notes.
License
© 2016 Scijs Authors. MIT License.
Authors
Ricky Reusser
