j6

j6 -- A JavaScript Scientific Library (like R, numPy, Matlab)

Introduction

The j6 is a A JavaScript Scientific Library like R.

It's based on lodash.js , jStat.js and numeric.js

Install

npm install j6

Use j6 in console mode

file : probabilityEx.js

var R = require("j6");
var dice = R.steps(1,6);
log("sample(1:6, 10)", R.samples(dice, 10));
log("runif(10,0,1)=", R.runif(10, 0, 1).str());
log("rnorm(10,5,1)=", R.rnorm(10, 5, 1).str());
log("dnorm(5,5,1)=", R.dnorm(5, 5, 1));
log("pnorm(5,5,1)=", R.pnorm(5, 5, 1));
log("qnorm(0.5,5,1)=", R.qnorm(0.5, 5, 1));
log("rbinom(10, 5, 0.5)=", R.rbinom(10,5,0.5));
log("dbinom(4, 5, 0.5)=", R.dbinom(4,5,0.5));
log("dbinom(5, 5, 0.5)=", R.dbinom(5,5,0.5));
log("pbinom(4, 5, 0.5)=", R.pbinom(4,5,0.5));
log("qbinom(0.9, 5, 0.5)=", R.qbinom(0.9,5,0.5));

run :

$ node probabilityEx.js
sample(1:6, 10) [ 3, 5, 3, 2, 3, 3, 1, 2, 4, 3 ]
runif(10,0,1)= [0.9119,0.5899,0.6839,0.1350,0.6894,0.9512,0.8186,0.5826,0.4279,0
.5125]
rnorm(10,5,1)= [5.8961,5.4312,6.0002,5.3623,5.5281,4.4413,6.2144,5.7173,5.3111,1
.3146]
dnorm(5,5,1)= 0.3989422804014327
pnorm(5,5,1)= 0.5
qnorm(0.5,5,1)= 5
rbinom(10, 5, 0.5)= [ 2, 1, 2, 2, 4, 4, 1, 4, 3, 2 ]
dbinom(4, 5, 0.5)= 0.15625
dbinom(5, 5, 0.5)= 0.03125
pbinom(4, 5, 0.5)= 0.96875
qbinom(0.9, 5, 0.5)= 4

file : statisticsEx.js

var R = require("j6");
var v = [1,3,5];
log("v.max()=", v.max());
log("v.min()=", v.min());
log("v.sum()=", v.sum());
log("v.normalize()=", v.normalize());
log("v.normalize().sum()=", v.normalize().sum());
log("v.product()=", v.product());
log("v.mean()=", v.mean());
log("v.range()=", v.range());
log("v.median()=", v.median());
log("v.variance()=", v.variance());
log("v.sd()=", v.sd(), " sd^2=", v.sd()*v.sd());
log("v.cov(v)=", v.cov(v), "v.cor(v)=", v.cor(v));
log("factorial(5)=", R.factorial(5));

run :

$ node statisticsEx.js
v.max()= 5
v.min()= 1
v.sum()= 9
v.normalize()= [ 0.1111111111111111, 0.3333333333333333, 0.5555555555555556 ]
v.normalize().sum()= 1
v.product()= 15
v.mean()= 1
v.range()= 4
v.median()= 3
v.variance()= 2.6666666666666665
v.sd()= 1.632993161855452  sd^2= 2.6666666666666665
v.cov(v)= 4 v.cor(v)= 1
factorial(5)= 120

file : testEx.js

var R = require("../j6");
var v = [1,3,5];
 
var x = R.rnorm(10, 0, 0.1);
print("x=", x.str());
 
var t1=R.ttest({x:x, mu:0});
R.report(t1);

run :

$ node testEx.js
x= [-0.1117,-0.1211,0.0382,-0.1902,0.0124,0.0949,0.2326,0.1315,-0.0261,0.0874]

=========== report ==========
name    : ttest(X)
h       : H0:mu=0
alpha   : 0.0500
op      : =
pvalue  : 0.7129
ci      : [-0.0733,0.1028]
df      : 9.0000
mean    : 0.0148
sd      : 0.1231

file : matrixEx.js

var M = require("j6").M;
var v = [1,2,3];
log("v.sin()=", v.sin());
log("v.norm2()=", v.norm2());
log("v.norm2Squared()=", v.norm2Squared());
 
var A = [[1,2,3],[4,5,6],[7,3,9]];
var AiA = A.inv().dot(A);
log("AiA=\n", AiA.strM());
log("AiA.tr()=\n", AiA.tr().strM());
log("A=\n", A.str());
log("A.mul(0.1)=\n", A.mul(0.1).strM());
log("A.row(1)=", A.row(1));
log("A.col(1)=", A.col(1));
log("A.sumM()=", A.sumM());
log("A.rowSum()=", A.rowSum());
log("A.colSum()=", A.colSum());
log("A.mean(row)=", A.rowMean().str());
log("A.mean(col)=", A.colMean().str());
 
var D = M.diag(v);
log("D=", D);
 
var Eλ = M.eigR(A);
var E = Eλ.E, λ=Eλ.lambda;
log("E*[λ]*E-1=", E.dot(λ.diag()).dot(E.inv()).strM());

run :

$ node matrixEx.js
v.sin()= [ 0.8414709848078965, 0.9092974268256817, 0.1411200080598672 ]
v.norm2()= 3.7416573867739413
v.norm2Squared()= 14
AiA=
 [[          1,   1.11e-16,  -1.11e-16],
 [          0,          1,  4.441e-16],
 [ -3.331e-16, -3.331e-16,          1]]
AiA.tr()=
 [[          1,          0, -3.331e-16],
 [   1.11e-16,          1, -3.331e-16],
 [  -1.11e-16,  4.441e-16,          1]]
A=
 [[1.0000,2.0000,3.0000],[4.0000,5.0000,6.0000],[7.0000,3.0000,9.0000]]
A.mul(0.1)=
 [[        0.1,        0.2,        0.3],
 [        0.4,        0.5,        0.6],
 [        0.7,        0.3,        0.9]]
A.row(1)= [ 4, 5, 6 ]
A.col(1)= [ 2, 5, 3 ]
A.sumM()= 40
A.rowSum(2)= [ 6, 15, 19 ]
A.colSum(2)= [ 12, 10, 18 ]
A.mean(row)= [2.0000,5.0000,6.3333]
A.mean(col)= [4.0000,3.3333,6.0000]
D= [ [ 1, 0, 0 ], [ 0, 2, 0 ], [ 0, 0, 3 ] ]
E*[λ]*E-1= [[          1,          2,          3],
 [          4,          5,          6],
 [          7,          3,          9]]

file : differentialEx.js

var R = require("j6");
 
var d = R.D.d, i=R.D.i, sin=R.sin, PI = R.PI, x2=(x)=>x*x;
 
log('d(x^2,2)=', d(x2, 2));
log('d(sin(x/4),pi/4)=', d(sin, PI/4));
log('i(x^2,0,1)=', i(x2,0,1));
log('i(sin(x),0,pi/2)=', i(sin,0,PI/2));
 

run :

D:\Dropbox\github\j6\example>node differentialEx.js
d(x^2,2)= 4.000999999999699
d(sin(x/4),pi/4)= 0.7067531099743674
i(x^2,0,1)= 0.33283350000000095
i(sin(x),0,pi/2)= 0.9997035898637557

file: symbolEx.js

var R = require("../j6");
var S = R.Symbol;
 
print('x+x=', S.run('x + x')) // => 2 x"
 
print('10!=', S.factor('10!').toString()); // => "2^8 3^4 5^2 7"
 
print('integral(x^2)=', S.eval('integral(x^2)').toString()); // => "1/3 x^3"
 
// composing...
print('integral(x)=', S.integral(S.eval('x')).toString()); // => "1/2 x^2"
 
var questions=[
'13579/99999 + 13580/100000',
'numerator(1/a+1/b)',
'denominator(1/(x-1)/(x-2))',
'rationalize(a/b+b/a)',
'A=1+i;B=sqrt(2)*exp(i*pi/4);A-B',
'simplify(cos(x)^2 + sin(x)^2)',
'simplify(a*b+a*c)',
'simplify(n!/(n+1)!)',
'(x-1)(x-2)^3',
'subst( u, exp(x), 2*exp(x) )',
'roots(3 x + 12 + y = 24)',
'roots(a*x^2+b*x+c)',
'roots(x^4 + x^3 + x^2 + x + 1)',
'roots(m*x^9 + n)',
'roots((x^4+x^3)*(x^4*x^2))',
'nroots(x^4+1)',
'velocity=17000*"mile"/"hr";time=8*"min"/(60*"min"/"hr");velocity/time',
'A=((a,b),(c,d));inv(A);adj(A);det(A);inv(A)-adj(A)/det(A)',
'd(x^2);r=sqrt(x^2+y^2);d(r,(x,y))',
'F=(x+2y,3x+4y);d(F,(x,y))',
'integral(x^2)',
'integral(x*y,x,y)',
// 'defint(x^2,y,0,sqrt(1-x^2),x,-1,1)', // very slow, why ?
// 'f=sin(t)^4-2*cos(t/2)^3*sin(t);f=circexp(f);defint(f,t,0,2*pi)', // very slow, why ?
];
 
print("=========== Q&A =============");
 
for (var i in questions) {
    var q = questions[i];
    print(q, "=", S.run(q.replace(/;/g, '\n')));
}

run :

D:\js\j6\example>node symbolEx.js
x+x= 2 x
10!= 2^8 3^4 5^2 7
integral(x^2)= 1/3 x^3
integral(x)= 1/2 x^2
=========== Q&A =============
13579/99999 + 13580/100000 = 135794321/499995000
numerator(1/a+1/b) = a + b
denominator(1/(x-1)/(x-2)) = x^2 - 3 x + 2
rationalize(a/b+b/a) = (a^2 + b^2) / (a b)
A=1+i;B=sqrt(2)*exp(i*pi/4);A-B = 1 + i - 2^(1/2) exp(1/4 i pi)
simplify(cos(x)^2 + sin(x)^2) = 1
simplify(a*b+a*c) = a (b + c)
simplify(n!/(n+1)!) = 1 / (1 + n)
(x-1)(x-2)^3 = x^4 - 7 x^3 + 18 x^2 - 20 x + 8
subst( u, exp(x), 2*exp(x) ) = 2 u
roots(3 x + 12 + y = 24) = -1/3 y + 4
roots(a*x^2+b*x+c) = (-b / (2 a) - (-4 a c + b^2)^(1/2) / (2 a),-b / (2 a) + (-4
 a c + b^2)^(1/2) / (2 a))
roots(x^4 + x^3 + x^2 + x + 1) = Stop: roots: the polynomial is not factorable,
try nroots
roots(m*x^9 + n) = Stop: roots: the polynomial is not factorable, try nroots
roots((x^4+x^3)*(x^4*x^2)) = (-1,0)
nroots(x^4+1) = (-0.707107 - 0.707107 i,-0.707107 + 0.707107 i,0.707107 + 0.7071
07 i,0.707107 - 0.707107 i)
velocity=17000*"mile"/"hr";time=8*"min"/(60*"min"/"hr");velocity/time = 127500 "
mile" / ("hr"^2)
A=((a,b),(c,d));inv(A);adj(A);det(A);inv(A)-adj(A)/det(A) = ((d / (a d - b c),-b
 / (a d - b c)),(-c / (a d - b c),a / (a d - b c)))
((d,-b),(-c,a))
a d - b c
((0,0),(0,0))
d(x^2);r=sqrt(x^2+y^2);d(r,(x,y)) = 2 x
(x / ((x^2 + y^2)^(1/2)),y / ((x^2 + y^2)^(1/2)))
F=(x+2y,3x+4y);d(F,(x,y)) = ((1,2),(3,4))
integral(x^2) = 1/3 x^3
integral(x*y,x,y) = 1/4 x^2 y^2

Run j6 on Web

There is a web IDE for j6 , just start the ide/j6.html for a demo.

You can start a server to use the IDE.

$ git clone https://github.com/ccckmit/j6
$ cd j6
$ npm install --dev
$ node server.js

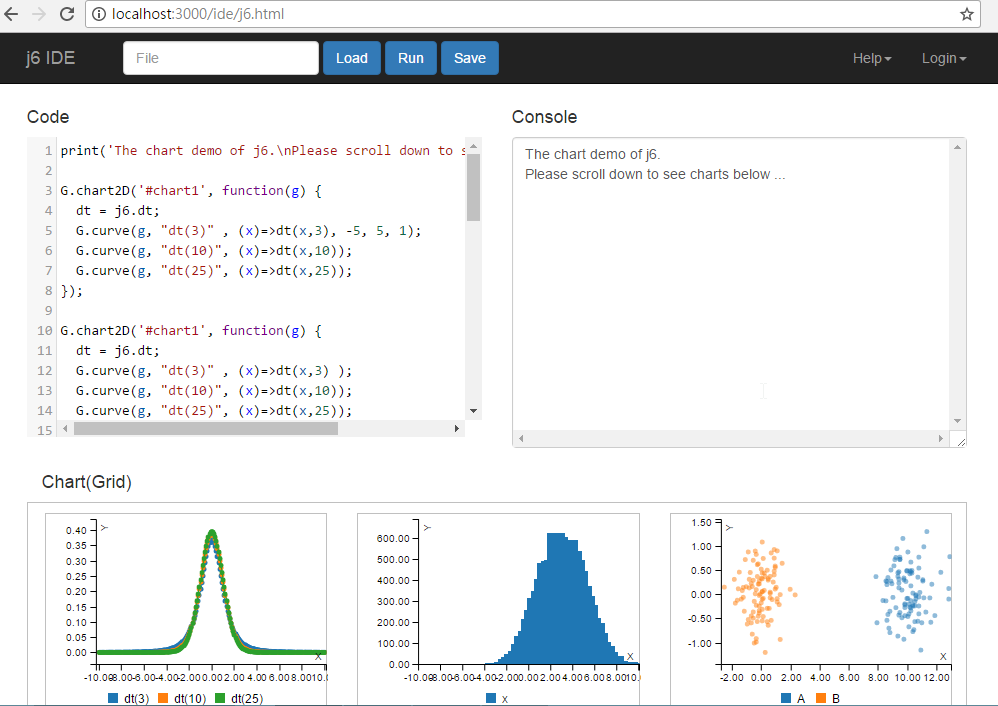
Visit http://localhost:3000/ide/j6.html for the j6 IDE。

A demo for j6 is on my web site https://mdbookspace.com/j6/ide/j6.html .

The following figure is Screen Shot for j6 GUI.

Rebuild Web Version

You have to rebuild j6 for web by browserify in the following command.

$npm run build-web

> j6@0.5.4 build-web D:\Dropbox\github\j6
> browserify web/_j6.js -o web/j6.js

When you modify the j6 source, make sure to rebuild it again.