d3-scale
Scales are a convenient abstraction for a fundamental task in visualization: mapping a dimension of abstract data to a visual representation. Although most often used for position-encoding quantitative data, such as mapping a measurement in meters to a position in pixels for dots in a scatterplot, scales can represent virtually any visual encoding, such as diverging colors, stroke widths, or symbol size. Scales can also be used with virtually any type of data, such as named categorical data or discrete data that requires sensible breaks.
For continuous quantitative data, you typically want a linear scale. (For time series data, a time scale.) If the distribution calls for it, consider transforming data using a power or log scale. A quantize scale may aid differentiation by rounding continuous data to a fixed set of discrete values; similarly, a quantile scale computes quantiles from a sample population, and a threshold scale allows you to specify arbitrary breaks in continuous data.
For discrete ordinal (ordered) or categorical (unordered) data, an ordinal scale specifies an explicit mapping from a set of data values to a corresponding set of visual attributes (such as colors). The related band and point scales are useful for position-encoding ordinal data, such as bars in a bar chart or dots in an categorical scatterplot.
This repository does not provide color schemes; see d3-scale-chromatic for color schemes designed to work with d3-scale.
Scales have no intrinsic visual representation. However, most scales can generate and format ticks for reference marks to aid in the construction of axes.
For a longer introduction, see these recommended tutorials:
-
Introducing d3-scale by Mike Bostock
-
Chapter 7. Scales of Interactive Data Visualization for the Web by Scott Murray
-
d3: scales, and color. by Jérôme Cukier
Installing
If you use npm, npm install d3-scale. You can also download the latest release on GitHub. For vanilla HTML in modern browsers, import d3-scale from Skypack:
<script type="module">
import {scaleLinear} from "https://cdn.skypack.dev/d3-scale@4";
const x = scaleLinear();
</script>For legacy environments, you can load d3-scale’s UMD bundle from an npm-based CDN such as jsDelivr; a d3 global is exported:
<script src="https://cdn.jsdelivr.net/npm/d3-array@3"></script>
<script src="https://cdn.jsdelivr.net/npm/d3-color@3"></script>
<script src="https://cdn.jsdelivr.net/npm/d3-format@3"></script>
<script src="https://cdn.jsdelivr.net/npm/d3-interpolate@3"></script>
<script src="https://cdn.jsdelivr.net/npm/d3-time@3"></script>
<script src="https://cdn.jsdelivr.net/npm/d3-time-format@4"></script>
<script src="https://cdn.jsdelivr.net/npm/d3-scale@4"></script>
<script>
const x = d3.scaleLinear();
</script>(You can omit d3-time and d3-time-format if you’re not using d3.scaleTime or d3.scaleUtc.)
API Reference
- Continuous (Linear, Power, Log, Identity, Time, Radial)
- Sequential
- Diverging
- Quantize
- Quantile
- Threshold
- Ordinal (Band, Point)
Continuous Scales
Continuous scales map a continuous, quantitative input domain to a continuous output range. If the range is also numeric, the mapping may be inverted. A continuous scale is not constructed directly; instead, try a linear, power, log, identity, radial, time or sequential color scale.
# continuous(value) · Source, Examples
Given a value from the domain, returns the corresponding value from the range. If the given value is outside the domain, and clamping is not enabled, the mapping may be extrapolated such that the returned value is outside the range. For example, to apply a position encoding:
var x = d3.scaleLinear()
.domain([10, 130])
.range([0, 960]);
x(20); // 80
x(50); // 320Or to apply a color encoding:
var color = d3.scaleLinear()
.domain([10, 100])
.range(["brown", "steelblue"]);
color(20); // "#9a3439"
color(50); // "#7b5167"Or, in shorthand:
var x = d3.scaleLinear([10, 130], [0, 960]);
var color = d3.scaleLinear([10, 100], ["brown", "steelblue"]);# continuous.invert(value) · Source, Examples
Given a value from the range, returns the corresponding value from the domain. Inversion is useful for interaction, say to determine the data value corresponding to the position of the mouse. For example, to invert a position encoding:
var x = d3.scaleLinear()
.domain([10, 130])
.range([0, 960]);
x.invert(80); // 20
x.invert(320); // 50If the given value is outside the range, and clamping is not enabled, the mapping may be extrapolated such that the returned value is outside the domain. This method is only supported if the range is numeric. If the range is not numeric, returns NaN.
For a valid value y in the range, continuous(continuous.invert(y)) approximately equals y; similarly, for a valid value x in the domain, continuous.invert(continuous(x)) approximately equals x. The scale and its inverse may not be exact due to the limitations of floating point precision.
# continuous.domain([domain]) · Source, Examples
If domain is specified, sets the scale’s domain to the specified array of numbers. The array must contain two or more elements. If the elements in the given array are not numbers, they will be coerced to numbers. If domain is not specified, returns a copy of the scale’s current domain.
Although continuous scales typically have two values each in their domain and range, specifying more than two values produces a piecewise scale. For example, to create a diverging color scale that interpolates between white and red for negative values, and white and green for positive values, say:
var color = d3.scaleLinear()
.domain([-1, 0, 1])
.range(["red", "white", "green"]);
color(-0.5); // "rgb(255, 128, 128)"
color(+0.5); // "rgb(128, 192, 128)"Internally, a piecewise scale performs a binary search for the range interpolator corresponding to the given domain value. Thus, the domain must be in ascending or descending order. If the domain and range have different lengths N and M, only the first min(N,M) elements in each are observed.
# continuous.range([range]) · Source, Examples
If range is specified, sets the scale’s range to the specified array of values. The array must contain two or more elements. Unlike the domain, elements in the given array need not be numbers; any value that is supported by the underlying interpolator will work, though note that numeric ranges are required for invert. If range is not specified, returns a copy of the scale’s current range. See continuous.interpolate for more examples.
# continuous.rangeRound([range]) · Source, Examples
Sets the scale’s range to the specified array of values while also setting the scale’s interpolator to interpolateRound. This is a convenience method equivalent to:
continuous
.range(range)
.interpolate(d3.interpolateRound);The rounding interpolator is sometimes useful for avoiding antialiasing artifacts, though also consider the shape-rendering “crispEdges” styles. Note that this interpolator can only be used with numeric ranges.
# continuous.clamp(clamp) · Source, Examples
If clamp is specified, enables or disables clamping accordingly. If clamping is disabled and the scale is passed a value outside the domain, the scale may return a value outside the range through extrapolation. If clamping is enabled, the return value of the scale is always within the scale’s range. Clamping similarly applies to continuous.invert. For example:
var x = d3.scaleLinear()
.domain([10, 130])
.range([0, 960]);
x(-10); // -160, outside range
x.invert(-160); // -10, outside domain
x.clamp(true);
x(-10); // 0, clamped to range
x.invert(-160); // 10, clamped to domainIf clamp is not specified, returns whether or not the scale currently clamps values to within the range.
# continuous.unknown([value]) · Source, Examples
If value is specified, sets the output value of the scale for undefined (or NaN) input values and returns this scale. If value is not specified, returns the current unknown value, which defaults to undefined.
# continuous.interpolate(interpolate) · Source, Examples
If interpolate is specified, sets the scale’s range interpolator factory. This interpolator factory is used to create interpolators for each adjacent pair of values from the range; these interpolators then map a normalized domain parameter t in [0, 1] to the corresponding value in the range. If factory is not specified, returns the scale’s current interpolator factory, which defaults to d3.interpolate. See d3-interpolate for more interpolators.
For example, consider a diverging color scale with three colors in the range:
var color = d3.scaleLinear()
.domain([-100, 0, +100])
.range(["red", "white", "green"]);Two interpolators are created internally by the scale, equivalent to:
var i0 = d3.interpolate("red", "white"),
i1 = d3.interpolate("white", "green");A common reason to specify a custom interpolator is to change the color space of interpolation. For example, to use HCL:
var color = d3.scaleLinear()
.domain([10, 100])
.range(["brown", "steelblue"])
.interpolate(d3.interpolateHcl);Or for Cubehelix with a custom gamma:
var color = d3.scaleLinear()
.domain([10, 100])
.range(["brown", "steelblue"])
.interpolate(d3.interpolateCubehelix.gamma(3));Note: the default interpolator may reuse return values. For example, if the range values are objects, then the value interpolator always returns the same object, modifying it in-place. If the scale is used to set an attribute or style, this is typically acceptable (and desirable for performance); however, if you need to store the scale’s return value, you must specify your own interpolator or make a copy as appropriate.
# continuous.ticks([count])
Returns approximately count representative values from the scale’s domain. If count is not specified, it defaults to 10. The returned tick values are uniformly spaced, have human-readable values (such as multiples of powers of 10), and are guaranteed to be within the extent of the domain. Ticks are often used to display reference lines, or tick marks, in conjunction with the visualized data. The specified count is only a hint; the scale may return more or fewer values depending on the domain. See also d3-array’s ticks.
# continuous.tickFormat([count[, specifier]]) · Source, Examples
Returns a number format function suitable for displaying a tick value, automatically computing the appropriate precision based on the fixed interval between tick values. The specified count should have the same value as the count that is used to generate the tick values.
An optional specifier allows a custom format where the precision of the format is automatically set by the scale as appropriate for the tick interval. For example, to format percentage change, you might say:
var x = d3.scaleLinear()
.domain([-1, 1])
.range([0, 960]);
var ticks = x.ticks(5),
tickFormat = x.tickFormat(5, "+%");
ticks.map(tickFormat); // ["-100%", "-50%", "+0%", "+50%", "+100%"]If specifier uses the format type s, the scale will return a SI-prefix format based on the largest value in the domain. If the specifier already specifies a precision, this method is equivalent to locale.format.
See also d3.tickFormat.
# continuous.nice([count]) · Source, Examples
Extends the domain so that it starts and ends on nice round values. This method typically modifies the scale’s domain, and may only extend the bounds to the nearest round value. An optional tick count argument allows greater control over the step size used to extend the bounds, guaranteeing that the returned ticks will exactly cover the domain. Nicing is useful if the domain is computed from data, say using extent, and may be irregular. For example, for a domain of [0.201479…, 0.996679…], a nice domain might be [0.2, 1.0]. If the domain has more than two values, nicing the domain only affects the first and last value. See also d3-array’s tickStep.
Nicing a scale only modifies the current domain; it does not automatically nice domains that are subsequently set using continuous.domain. You must re-nice the scale after setting the new domain, if desired.
# continuous.copy() · Source, Examples
Returns an exact copy of this scale. Changes to this scale will not affect the returned scale, and vice versa.
# d3.tickFormat(start, stop, count[, specifier]) · Source, Examples
Returns a number format function suitable for displaying a tick value, automatically computing the appropriate precision based on the fixed interval between tick values, as determined by d3.tickStep.
An optional specifier allows a custom format where the precision of the format is automatically set by the scale as appropriate for the tick interval. For example, to format percentage change, you might say:
var tickFormat = d3.tickFormat(-1, 1, 5, "+%");
tickFormat(-0.5); // "-50%"If specifier uses the format type s, the scale will return a SI-prefix format based on the larger absolute value of start and stop. If the specifier already specifies a precision, this method is equivalent to locale.format.
Linear Scales
# d3.scaleLinear([[domain, ]range]) · Source, Examples
Constructs a new continuous scale with the specified domain and range, the default interpolator and clamping disabled. If either domain or range are not specified, each defaults to [0, 1]. Linear scales are a good default choice for continuous quantitative data because they preserve proportional differences. Each range value y can be expressed as a function of the domain value x: y = mx + b.
Power Scales
Power scales are similar to linear scales, except an exponential transform is applied to the input domain value before the output range value is computed. Each range value y can be expressed as a function of the domain value x: y = mx^k + b, where k is the exponent value. Power scales also support negative domain values, in which case the input value and the resulting output value are multiplied by -1.
# d3.scalePow([[domain, ]range]) · Source, Examples
Constructs a new continuous scale with the specified domain and range, the exponent 1, the default interpolator and clamping disabled. If either domain or range are not specified, each defaults to [0, 1]. (Note that this is effectively a linear scale until you set a different exponent.)
# pow(value) · Source, Examples
See continuous.
# pow.invert(value) · Source, Examples
See continuous.invert.
# pow.exponent([exponent]) · Source, Examples
If exponent is specified, sets the current exponent to the given numeric value. If exponent is not specified, returns the current exponent, which defaults to 1. (Note that this is effectively a linear scale until you set a different exponent.)
# pow.domain([domain]) · Source, Examples
See continuous.domain.
# pow.range([range]) · Source, Examples
See continuous.range.
# pow.rangeRound([range]) · Source, Examples
# pow.clamp(clamp) · Source, Examples
See continuous.clamp.
# pow.interpolate(interpolate) · Source, Examples
# pow.ticks([count]) · Source, Examples
See continuous.ticks.
# pow.tickFormat([count[, specifier]]) · Source, Examples
# pow.nice([count]) · Source, Examples
See continuous.nice.
# pow.copy() · Source, Examples
See continuous.copy.
# d3.scaleSqrt([[domain, ]range]) · Source, Examples
Constructs a new continuous power scale with the specified domain and range, the exponent 0.5, the default interpolator and clamping disabled. If either domain or range are not specified, each defaults to [0, 1]. This is a convenience method equivalent to d3.scalePow(…).exponent(0.5).
Log Scales
Log scales are similar to linear scales, except a logarithmic transform is applied to the input domain value before the output range value is computed. The mapping to the range value y can be expressed as a function of the domain value x: y = m log(x) + b.
As log(0) = -∞, a log scale domain must be strictly-positive or strictly-negative; the domain must not include or cross zero. A log scale with a positive domain has a well-defined behavior for positive values, and a log scale with a negative domain has a well-defined behavior for negative values. (For a negative domain, input and output values are implicitly multiplied by -1.) The behavior of the scale is undefined if you pass a negative value to a log scale with a positive domain or vice versa.
# d3.scaleLog([[domain, ]range]) · Source, Examples
Constructs a new continuous scale with the specified domain and range, the base 10, the default interpolator and clamping disabled. If domain is not specified, it defaults to [1, 10]. If range is not specified, it defaults to [0, 1].
# log(value) · Source, Examples
See continuous.
# log.invert(value) · Source, Examples
See continuous.invert.
# log.base([base]) · Source, Examples
If base is specified, sets the base for this logarithmic scale to the specified value. If base is not specified, returns the current base, which defaults to 10.
# log.domain([domain]) · Source, Examples
See continuous.domain.
# log.range([range]) · Source, Examples
See continuous.range.
# log.rangeRound([range]) · Source, Examples
# log.clamp(clamp) · Source, Examples
See continuous.clamp.
# log.interpolate(interpolate) · Source, Examples
# log.ticks([count]) · Source, Examples
Like continuous.ticks, but customized for a log scale. If the base is an integer, the returned ticks are uniformly spaced within each integer power of base; otherwise, one tick per power of base is returned. The returned ticks are guaranteed to be within the extent of the domain. If the orders of magnitude in the domain is greater than count, then at most one tick per power is returned. Otherwise, the tick values are unfiltered, but note that you can use log.tickFormat to filter the display of tick labels. If count is not specified, it defaults to 10.
# log.tickFormat([count[, specifier]]) · Source, Examples
Like continuous.tickFormat, but customized for a log scale. The specified count typically has the same value as the count that is used to generate the tick values. If there are too many ticks, the formatter may return the empty string for some of the tick labels; however, note that the ticks are still shown. To disable filtering, specify a count of Infinity. When specifying a count, you may also provide a format specifier or format function. For example, to get a tick formatter that will display 20 ticks of a currency, say log.tickFormat(20, "$,f"). If the specifier does not have a defined precision, the precision will be set automatically by the scale, returning the appropriate format. This provides a convenient way of specifying a format whose precision will be automatically set by the scale.
# log.nice() · Source, Examples
Like continuous.nice, except extends the domain to integer powers of base. For example, for a domain of [0.201479…, 0.996679…], and base 10, the nice domain is [0.1, 1]. If the domain has more than two values, nicing the domain only affects the first and last value.
# log.copy() · Source, Examples
See continuous.copy.
Symlog Scales
See A bi-symmetric log transformation for wide-range data by Webber for more.
# d3.scaleSymlog([[domain, ]range]) · Source, Examples
Constructs a new continuous scale with the specified domain and range, the constant 1, the default interpolator and clamping disabled. If domain is not specified, it defaults to [0, 1]. If range is not specified, it defaults to [0, 1].
# symlog.constant([constant]) · Source, Examples
If constant is specified, sets the symlog constant to the specified number and returns this scale; otherwise returns the current value of the symlog constant, which defaults to 1. See “A bi-symmetric log transformation for wide-range data” by Webber for more.
Identity Scales
Identity scales are a special case of linear scales where the domain and range are identical; the scale and its invert method are thus the identity function. These scales are occasionally useful when working with pixel coordinates, say in conjunction with an axis. Identity scales do not support rangeRound, clamp or interpolate.
# d3.scaleIdentity([range]) · Source, Examples
Constructs a new identity scale with the specified domain and range. If range is not specified, it defaults to [0, 1].
Radial Scales
Radial scales are a variant of linear scales where the range is internally squared so that an input value corresponds linearly to the squared output value. These scales are useful when you want the input value to correspond to the area of a graphical mark and the mark is specified by radius, as in a radial bar chart. Radial scales do not support interpolate.
# d3.scaleRadial([[domain, ]range]) · Source, Examples
Constructs a new radial scale with the specified domain and range. If domain or range is not specified, each defaults to [0, 1].
Time Scales
Time scales are a variant of linear scales that have a temporal domain: domain values are coerced to dates rather than numbers, and invert likewise returns a date. Time scales implement ticks based on calendar intervals, taking the pain out of generating axes for temporal domains.
For example, to create a position encoding:
var x = d3.scaleTime()
.domain([new Date(2000, 0, 1), new Date(2000, 0, 2)])
.range([0, 960]);
x(new Date(2000, 0, 1, 5)); // 200
x(new Date(2000, 0, 1, 16)); // 640
x.invert(200); // Sat Jan 01 2000 05:00:00 GMT-0800 (PST)
x.invert(640); // Sat Jan 01 2000 16:00:00 GMT-0800 (PST)For a valid value y in the range, time(time.invert(y)) equals y; similarly, for a valid value x in the domain, time.invert(time(x)) equals x. The invert method is useful for interaction, say to determine the value in the domain that corresponds to the pixel location under the mouse.
# d3.scaleTime([[domain, ]range]) · Source, Examples
Constructs a new time scale with the specified domain and range, the default interpolator and clamping disabled. If domain is not specified, it defaults to [2000-01-01, 2000-01-02]. If range is not specified, it defaults to [0, 1].
# time(value) · Source, Examples
See continuous.
# time.invert(value) · Source, Examples
See continuous.invert.
# time.domain([domain]) · Source, Examples
See continuous.domain.
# time.range([range]) · Source, Examples
See continuous.range.
# time.rangeRound([range]) · Source, Examples
# time.clamp(clamp) · Source, Examples
See continuous.clamp.
# time.interpolate(interpolate) · Source, Examples
# time.ticks([count]) · Source, Examples
# time.ticks([interval])
Returns representative dates from the scale’s domain. The returned tick values are uniformly-spaced (mostly), have sensible values (such as every day at midnight), and are guaranteed to be within the extent of the domain. Ticks are often used to display reference lines, or tick marks, in conjunction with the visualized data.
An optional count may be specified to affect how many ticks are generated. If count is not specified, it defaults to 10. The specified count is only a hint; the scale may return more or fewer values depending on the domain. For example, to create ten default ticks, say:
var x = d3.scaleTime();
x.ticks(10);
// [Sat Jan 01 2000 00:00:00 GMT-0800 (PST),
// Sat Jan 01 2000 03:00:00 GMT-0800 (PST),
// Sat Jan 01 2000 06:00:00 GMT-0800 (PST),
// Sat Jan 01 2000 09:00:00 GMT-0800 (PST),
// Sat Jan 01 2000 12:00:00 GMT-0800 (PST),
// Sat Jan 01 2000 15:00:00 GMT-0800 (PST),
// Sat Jan 01 2000 18:00:00 GMT-0800 (PST),
// Sat Jan 01 2000 21:00:00 GMT-0800 (PST),
// Sun Jan 02 2000 00:00:00 GMT-0800 (PST)]The following time intervals are considered for automatic ticks:
- 1-, 5-, 15- and 30-second.
- 1-, 5-, 15- and 30-minute.
- 1-, 3-, 6- and 12-hour.
- 1- and 2-day.
- 1-week.
- 1- and 3-month.
- 1-year.
In lieu of a count, a time interval may be explicitly specified. To prune the generated ticks for a given time interval, use interval.every. For example, to generate ticks at 15-minute intervals:
var x = d3.scaleTime()
.domain([new Date(2000, 0, 1, 0), new Date(2000, 0, 1, 2)]);
x.ticks(d3.timeMinute.every(15));
// [Sat Jan 01 2000 00:00:00 GMT-0800 (PST),
// Sat Jan 01 2000 00:15:00 GMT-0800 (PST),
// Sat Jan 01 2000 00:30:00 GMT-0800 (PST),
// Sat Jan 01 2000 00:45:00 GMT-0800 (PST),
// Sat Jan 01 2000 01:00:00 GMT-0800 (PST),
// Sat Jan 01 2000 01:15:00 GMT-0800 (PST),
// Sat Jan 01 2000 01:30:00 GMT-0800 (PST),
// Sat Jan 01 2000 01:45:00 GMT-0800 (PST),
// Sat Jan 01 2000 02:00:00 GMT-0800 (PST)]Alternatively, pass a test function to interval.filter:
x.ticks(d3.timeMinute.filter(function(d) {
return d.getMinutes() % 15 === 0;
}));Note: in some cases, such as with day ticks, specifying a step can result in irregular spacing of ticks because time intervals have varying length.
# time.tickFormat([count[, specifier]]) · Source, Examples
# time.tickFormat([interval[, specifier]])
Returns a time format function suitable for displaying tick values. The specified count or interval is currently ignored, but is accepted for consistency with other scales such as continuous.tickFormat. If a format specifier is specified, this method is equivalent to format. If specifier is not specified, the default time format is returned. The default multi-scale time format chooses a human-readable representation based on the specified date as follows:
-
%Y- for year boundaries, such as2011. -
%B- for month boundaries, such asFebruary. -
%b %d- for week boundaries, such asFeb 06. -
%a %d- for day boundaries, such asMon 07. -
%I %p- for hour boundaries, such as01 AM. -
%I:%M- for minute boundaries, such as01:23. -
:%S- for second boundaries, such as:45. -
.%L- milliseconds for all other times, such as.012.
Although somewhat unusual, this default behavior has the benefit of providing both local and global context: for example, formatting a sequence of ticks as [11 PM, Mon 07, 01 AM] reveals information about hours, dates, and day simultaneously, rather than just the hours [11 PM, 12 AM, 01 AM]. See d3-time-format if you’d like to roll your own conditional time format.
# time.nice([count]) · Source, Examples
# time.nice([interval])
Extends the domain so that it starts and ends on nice round values. This method typically modifies the scale’s domain, and may only extend the bounds to the nearest round value. See continuous.nice for more.
An optional tick count argument allows greater control over the step size used to extend the bounds, guaranteeing that the returned ticks will exactly cover the domain. Alternatively, a time interval may be specified to explicitly set the ticks. If an interval is specified, an optional step may also be specified to skip some ticks. For example, time.nice(d3.timeSecond.every(10)) will extend the domain to an even ten seconds (0, 10, 20, etc.). See time.ticks and interval.every for further detail.
Nicing is useful if the domain is computed from data, say using extent, and may be irregular. For example, for a domain of [2009-07-13T00:02, 2009-07-13T23:48], the nice domain is [2009-07-13, 2009-07-14]. If the domain has more than two values, nicing the domain only affects the first and last value.
# time.copy() · Source, Examples
See continuous.copy.
# d3.scaleUtc([[domain, ]range]) · Source, Examples
Equivalent to scaleTime, but the returned time scale operates in Coordinated Universal Time rather than local time.
Sequential Scales
Sequential scales, like diverging scales, are similar to continuous scales in that they map a continuous, numeric input domain to a continuous output range. However, unlike continuous scales, the input domain and output range of a sequential scale always has exactly two elements, and the output range is typically specified as an interpolator rather than an array of values. These scales do not expose invert and interpolate methods.
# d3.scaleSequential([[domain, ]interpolator]) · Source, Examples
Constructs a new sequential scale with the specified domain and interpolator function or array. If domain is not specified, it defaults to [0, 1]. If interpolator is not specified, it defaults to the identity function. When the scale is applied, the interpolator will be invoked with a value typically in the range [0, 1], where 0 represents the minimum value and 1 represents the maximum value. For example, to implement the ill-advised HSL rainbow scale:
var rainbow = d3.scaleSequential(function(t) {
return d3.hsl(t * 360, 1, 0.5) + "";
});A more aesthetically-pleasing and perceptually-effective cyclical hue encoding is to use d3.interpolateRainbow:
var rainbow = d3.scaleSequential(d3.interpolateRainbow);If interpolator is an array, it represents the scale’s two-element output range and is converted to an interpolator function using d3.interpolate.
# sequential(value) · Source, Examples
See continuous.
# sequential.domain([domain]) · Source, Examples
See continuous.domain. Note that a sequential scale’s domain must be numeric and must contain exactly two values.
# sequential.clamp([clamp]) · Source, Examples
See continuous.clamp.
# sequential.interpolator([interpolator]) · Source, Examples
If interpolator is specified, sets the scale’s interpolator to the specified function. If interpolator is not specified, returns the scale’s current interpolator.
# sequential.range([range]) · Source, Examples
See continuous.range. If range is specified, the given two-element array is converted to an interpolator function using d3.interpolate.
# sequential.rangeRound([range]) · Source, Examples
See continuous.rangeRound. If range is specified, implicitly uses d3.interpolateRound as the interpolator.
# sequential.copy() · Source, Examples
See continuous.copy.
# d3.scaleSequentialLog([[domain, ]range]) · Source, Examples
A sequential scale with a logarithmic transform, analogous to a log scale.
# d3.scaleSequentialPow([[domain, ]range]) · Source, Examples
A sequential scale with an exponential transform, analogous to a power scale.
# d3.scaleSequentialSqrt([[domain, ]range]) · Source, Examples
A sequential scale with a square-root transform, analogous to a d3.scaleSqrt.
# d3.scaleSequentialSymlog([[domain, ]range]) · Source, Examples
A sequential scale with a symmetric logarithmic transform, analogous to a symlog scale.
# d3.scaleSequentialQuantile([[domain, ]range]) · Source, Examples
A sequential scale using a p-quantile transform, analogous to a quantile scale.
# sequentialQuantile.quantiles(n) · Source, Examples
Returns an array of n + 1 quantiles. For example, if n = 4, returns an array of five numbers: the minimum value, the first quartile, the median, the third quartile, and the maximum.
Diverging Scales
Diverging scales, like sequential scales, are similar to continuous scales in that they map a continuous, numeric input domain to a continuous output range. However, unlike continuous scales, the input domain and output range of a diverging scale always has exactly three elements, and the output range is typically specified as an interpolator rather than an array of values. These scales do not expose invert and interpolate methods.
# d3.scaleDiverging([[domain, ]interpolator]) · Source, Examples
Constructs a new diverging scale with the specified domain and interpolator function or array. If domain is not specified, it defaults to [0, 0.5, 1]. If interpolator is not specified, it defaults to the identity function. When the scale is applied, the interpolator will be invoked with a value typically in the range [0, 1], where 0 represents the extreme negative value, 0.5 represents the neutral value, and 1 represents the extreme positive value. For example, using d3.interpolateSpectral:
var spectral = d3.scaleDiverging(d3.interpolateSpectral);If interpolator is an array, it represents the scale’s three-element output range and is converted to an interpolator function using d3.interpolate and d3.piecewise.
# diverging(value) · Source, Examples
See continuous.
# diverging.domain([domain]) · Source, Examples
See continuous.domain. Note that a diverging scale’s domain must be numeric and must contain exactly three values. The default domain is [0, 0.5, 1].
# diverging.clamp([clamp]) · Source, Examples
See continuous.clamp.
# diverging.interpolator([interpolator]) · Source, Examples
If interpolator is specified, sets the scale’s interpolator to the specified function. If interpolator is not specified, returns the scale’s current interpolator.
# diverging.range([range]) · Source, Examples
See continuous.range. If range is specified, the given three-element array is converted to an interpolator function using d3.interpolate and d3.piecewise.
# diverging.rangeRound([range]) · Source, Examples
See continuous.range. If range is specified, implicitly uses d3.interpolateRound as the interpolator.
# diverging.copy() · Source, Examples
See continuous.copy.
# diverging.unknown() · Source, Examples
See continuous.unknown.
# d3.scaleDivergingLog([[domain, ]range]) · Source, Examples
A diverging scale with a logarithmic transform, analogous to a log scale.
# d3.scaleDivergingPow([[domain, ]range]) · Source, Examples
A diverging scale with an exponential transform, analogous to a power scale.
# d3.scaleDivergingSqrt([[domain, ]range]) · Source, Examples
A diverging scale with a square-root transform, analogous to a d3.scaleSqrt.
# d3.scaleDivergingSymlog([[domain, ]range]) · Source, Examples
A diverging scale with a symmetric logarithmic transform, analogous to a symlog scale.
Quantize Scales
Quantize scales are similar to linear scales, except they use a discrete rather than continuous range. The continuous input domain is divided into uniform segments based on the number of values in (i.e., the cardinality of) the output range. Each range value y can be expressed as a quantized linear function of the domain value x: y = m round(x) + b. See this choropleth for an example.
# d3.scaleQuantize([[domain, ]range]) · Source, Examples
Constructs a new quantize scale with the specified domain and range. If either domain or range is not specified, each defaults to [0, 1]. Thus, the default quantize scale is equivalent to the Math.round function.
# quantize(value) · Source, Examples
Given a value in the input domain, returns the corresponding value in the output range. For example, to apply a color encoding:
var color = d3.scaleQuantize()
.domain([0, 1])
.range(["brown", "steelblue"]);
color(0.49); // "brown"
color(0.51); // "steelblue"Or dividing the domain into three equally-sized parts with different range values to compute an appropriate stroke width:
var width = d3.scaleQuantize()
.domain([10, 100])
.range([1, 2, 4]);
width(20); // 1
width(50); // 2
width(80); // 4# quantize.invertExtent(value) · Source, Examples
Returns the extent of values in the domain [x0, x1] for the corresponding value in the range: the inverse of quantize. This method is useful for interaction, say to determine the value in the domain that corresponds to the pixel location under the mouse.
var width = d3.scaleQuantize()
.domain([10, 100])
.range([1, 2, 4]);
width.invertExtent(2); // [40, 70]# quantize.domain([domain]) · Source, Examples
If domain is specified, sets the scale’s domain to the specified two-element array of numbers. If the elements in the given array are not numbers, they will be coerced to numbers. The numbers must be in ascending order or the behavior of the scale is undefined. If domain is not specified, returns the scale’s current domain.
# quantize.range([range]) · Source, Examples
If range is specified, sets the scale’s range to the specified array of values. The array may contain any number of discrete values. The elements in the given array need not be numbers; any value or type will work. If range is not specified, returns the scale’s current range.
# quantize.ticks([count]) · Source, Examples
Equivalent to continuous.ticks.
# quantize.tickFormat([count[, specifier]]) · Source, Examples
Equivalent to continuous.tickFormat.
# quantize.nice() · Source, Examples
Equivalent to continuous.nice.
# quantize.thresholds() · Source, Examples
Returns the array of computed thresholds within the domain.
# quantize.copy() · Source, Examples
Returns an exact copy of this scale. Changes to this scale will not affect the returned scale, and vice versa.
Quantile Scales
Quantile scales map a sampled input domain to a discrete range. The domain is considered continuous and thus the scale will accept any reasonable input value; however, the domain is specified as a discrete set of sample values. The number of values in (the cardinality of) the output range determines the number of quantiles that will be computed from the domain. To compute the quantiles, the domain is sorted, and treated as a population of discrete values; see d3-array’s quantile. See this quantile choropleth for an example.
# d3.scaleQuantile([[domain, ]range]) · Source, Examples
Constructs a new quantile scale with the specified domain and range. If either domain or range is not specified, each defaults to the empty array. The quantile scale is invalid until both a domain and range are specified.
# quantile(value) · Source, Examples
Given a value in the input domain, returns the corresponding value in the output range.
# quantile.invertExtent(value) · Source, Examples
Returns the extent of values in the domain [x0, x1] for the corresponding value in the range: the inverse of quantile. This method is useful for interaction, say to determine the value in the domain that corresponds to the pixel location under the mouse.
# quantile.domain([domain]) · Source, Examples
If domain is specified, sets the domain of the quantile scale to the specified set of discrete numeric values. The array must not be empty, and must contain at least one numeric value; NaN, null and undefined values are ignored and not considered part of the sample population. If the elements in the given array are not numbers, they will be coerced to numbers. A copy of the input array is sorted and stored internally. If domain is not specified, returns the scale’s current domain.
# quantile.range([range]) · Source, Examples
If range is specified, sets the discrete values in the range. The array must not be empty, and may contain any type of value. The number of values in (the cardinality, or length, of) the range array determines the number of quantiles that are computed. For example, to compute quartiles, range must be an array of four elements such as [0, 1, 2, 3]. If range is not specified, returns the current range.
# quantile.quantiles() · Source, Examples
Returns the quantile thresholds. If the range contains n discrete values, the returned array will contain n - 1 thresholds. Values less than the first threshold are considered in the first quantile; values greater than or equal to the first threshold but less than the second threshold are in the second quantile, and so on. Internally, the thresholds array is used with bisect to find the output quantile associated with the given input value.
# quantile.copy() · Source, Examples
Returns an exact copy of this scale. Changes to this scale will not affect the returned scale, and vice versa.
Threshold Scales
Threshold scales are similar to quantize scales, except they allow you to map arbitrary subsets of the domain to discrete values in the range. The input domain is still continuous, and divided into slices based on a set of threshold values. See this choropleth for an example.
# d3.scaleThreshold([[domain, ]range]) · Source, Examples
Constructs a new threshold scale with the specified domain and range. If domain is not specified, it defaults to [0.5]. If range is not specified, it defaults to [0, 1]. Thus, the default threshold scale is equivalent to the Math.round function for numbers; for example threshold(0.49) returns 0, and threshold(0.51) returns 1.
# threshold(value) · Source, Examples
Given a value in the input domain, returns the corresponding value in the output range. For example:
var color = d3.scaleThreshold()
.domain([0, 1])
.range(["red", "white", "green"]);
color(-1); // "red"
color(0); // "white"
color(0.5); // "white"
color(1); // "green"
color(1000); // "green"# threshold.invertExtent(value) · Source, Examples
Returns the extent of values in the domain [x0, x1] for the corresponding value in the range, representing the inverse mapping from range to domain. This method is useful for interaction, say to determine the value in the domain that corresponds to the pixel location under the mouse. For example:
var color = d3.scaleThreshold()
.domain([0, 1])
.range(["red", "white", "green"]);
color.invertExtent("red"); // [undefined, 0]
color.invertExtent("white"); // [0, 1]
color.invertExtent("green"); // [1, undefined]# threshold.domain([domain]) · Source, Examples
If domain is specified, sets the scale’s domain to the specified array of values. The values must be in ascending order or the behavior of the scale is undefined. The values are typically numbers, but any naturally ordered values (such as strings) will work; a threshold scale can be used to encode any type that is ordered. If the number of values in the scale’s range is N+1, the number of values in the scale’s domain must be N. If there are fewer than N elements in the domain, the additional values in the range are ignored. If there are more than N elements in the domain, the scale may return undefined for some inputs. If domain is not specified, returns the scale’s current domain.
# threshold.range([range]) · Source, Examples
If range is specified, sets the scale’s range to the specified array of values. If the number of values in the scale’s domain is N, the number of values in the scale’s range must be N+1. If there are fewer than N+1 elements in the range, the scale may return undefined for some inputs. If there are more than N+1 elements in the range, the additional values are ignored. The elements in the given array need not be numbers; any value or type will work. If range is not specified, returns the scale’s current range.
# threshold.copy() · Source, Examples
Returns an exact copy of this scale. Changes to this scale will not affect the returned scale, and vice versa.
Ordinal Scales
Unlike continuous scales, ordinal scales have a discrete domain and range. For example, an ordinal scale might map a set of named categories to a set of colors, or determine the horizontal positions of columns in a column chart.
# d3.scaleOrdinal([[domain, ]range]) · Source, Examples
Constructs a new ordinal scale with the specified domain and range. If domain is not specified, it defaults to the empty array. If range is not specified, it defaults to the empty array; an ordinal scale always returns undefined until a non-empty range is defined.
# ordinal(value) · Source, Examples
Given a value in the input domain, returns the corresponding value in the output range. If the given value is not in the scale’s domain, returns the unknown; or, if the unknown value is implicit (the default), then the value is implicitly added to the domain and the next-available value in the range is assigned to value, such that this and subsequent invocations of the scale given the same input value return the same output value.
# ordinal.domain([domain]) · Source, Examples
If domain is specified, sets the domain to the specified array of values. The first element in domain will be mapped to the first element in the range, the second domain value to the second range value, and so on. Domain values are stored internally in an InternMap from primitive value to index; the resulting index is then used to retrieve a value from the range. Thus, an ordinal scale’s values must be coercible to a primitive value, and the primitive domain value uniquely identifies the corresponding range value. If domain is not specified, this method returns the current domain.
Setting the domain on an ordinal scale is optional if the unknown value is implicit (the default). In this case, the domain will be inferred implicitly from usage by assigning each unique value passed to the scale a new value from the range. Note that an explicit domain is recommended to ensure deterministic behavior, as inferring the domain from usage will be dependent on ordering.
# ordinal.range([range]) · Source, Examples
If range is specified, sets the range of the ordinal scale to the specified array of values. The first element in the domain will be mapped to the first element in range, the second domain value to the second range value, and so on. If there are fewer elements in the range than in the domain, the scale will reuse values from the start of the range. If range is not specified, this method returns the current range.
# ordinal.unknown([value]) · Source, Examples
If value is specified, sets the output value of the scale for unknown input values and returns this scale. If value is not specified, returns the current unknown value, which defaults to implicit. The implicit value enables implicit domain construction; see ordinal.domain.
# ordinal.copy() · Source, Examples
Returns an exact copy of this ordinal scale. Changes to this scale will not affect the returned scale, and vice versa.
# d3.scaleImplicit · Source, Examples
A special value for ordinal.unknown that enables implicit domain construction: unknown values are implicitly added to the domain.
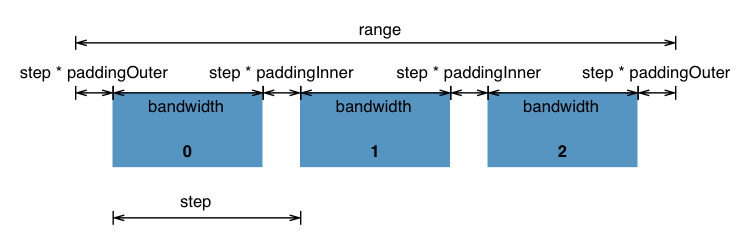
Band Scales
Band scales are like ordinal scales except the output range is continuous and numeric. Discrete output values are automatically computed by the scale by dividing the continuous range into uniform bands. Band scales are typically used for bar charts with an ordinal or categorical dimension. The unknown value of a band scale is effectively undefined: they do not allow implicit domain construction.
# d3.scaleBand([[domain, ]range]) · Source, Examples
Constructs a new band scale with the specified domain and range, no padding, no rounding and center alignment. If domain is not specified, it defaults to the empty domain. If range is not specified, it defaults to the unit range [0, 1].
# band(value) · Source, Examples
Given a value in the input domain, returns the start of the corresponding band derived from the output range. If the given value is not in the scale’s domain, returns undefined.
# band.domain([domain]) · Source, Examples
If domain is specified, sets the domain to the specified array of values. The first element in domain will be mapped to the first band, the second domain value to the second band, and so on. Domain values are stored internally in an InternMap from primitive value to index; the resulting index is then used to determine the band. Thus, a band scale’s values must be coercible to a primitive value, and the primitive domain value uniquely identifies the corresponding band. If domain is not specified, this method returns the current domain.
# band.range([range]) · Source, Examples
If range is specified, sets the scale’s range to the specified two-element array of numbers. If the elements in the given array are not numbers, they will be coerced to numbers. If range is not specified, returns the scale’s current range, which defaults to [0, 1].
# band.rangeRound([range]) · Source, Examples
Sets the scale’s range to the specified two-element array of numbers while also enabling rounding. This is a convenience method equivalent to:
band
.range(range)
.round(true);Rounding is sometimes useful for avoiding antialiasing artifacts, though also consider the shape-rendering “crispEdges” styles.
# band.round([round]) · Source, Examples
If round is specified, enables or disables rounding accordingly. If rounding is enabled, the start and stop of each band will be integers. Rounding is sometimes useful for avoiding antialiasing artifacts, though also consider the shape-rendering “crispEdges” styles. Note that if the width of the domain is not a multiple of the cardinality of the range, there may be leftover unused space, even without padding! Use band.align to specify how the leftover space is distributed.
# band.paddingInner([padding]) · Source, Examples
If padding is specified, sets the inner padding to the specified number which must be less than or equal to 1. If padding is not specified, returns the current inner padding which defaults to 0. The inner padding specifies the proportion of the range that is reserved for blank space between bands; a value of 0 means no blank space between bands, and a value of 1 means a bandwidth of zero.
# band.paddingOuter([padding]) · Source, Examples
If padding is specified, sets the outer padding to the specified number which is typically in the range [0, 1]. If padding is not specified, returns the current outer padding which defaults to 0. The outer padding specifies the amount of blank space, in terms of multiples of the step, to reserve before the first band and after the last band.
# band.padding([padding]) · Source, Examples
A convenience method for setting the inner and outer padding to the same padding value. If padding is not specified, returns the inner padding.
# band.align([align]) · Source, Examples
If align is specified, sets the alignment to the specified value which must be in the range [0, 1]. If align is not specified, returns the current alignment which defaults to 0.5. The alignment specifies how outer padding is distributed in the range. A value of 0.5 indicates that the outer padding should be equally distributed before the first band and after the last band; i.e., the bands should be centered within the range. A value of 0 or 1 may be used to shift the bands to one side, say to position them adjacent to an axis. For more, see this explainer.
# band.bandwidth() · Source, Examples
Returns the width of each band.
# band.step() · Source, Examples
Returns the distance between the starts of adjacent bands.
# band.copy() · Source, Examples
Returns an exact copy of this scale. Changes to this scale will not affect the returned scale, and vice versa.
Point Scales
Point scales are a variant of band scales with the bandwidth fixed to zero. Point scales are typically used for scatterplots with an ordinal or categorical dimension. The unknown value of a point scale is always undefined: they do not allow implicit domain construction.
# d3.scalePoint([[domain, ]range]) · Source, Examples
Constructs a new point scale with the specified domain and range, no padding, no rounding and center alignment. If domain is not specified, it defaults to the empty domain. If range is not specified, it defaults to the unit range [0, 1].
# point(value) · Source, Examples
Given a value in the input domain, returns the corresponding point derived from the output range. If the given value is not in the scale’s domain, returns undefined.
# point.domain([domain]) · Source, Examples
If domain is specified, sets the domain to the specified array of values. The first element in domain will be mapped to the first point, the second domain value to the second point, and so on. Domain values are stored internally in an InternMap from primitive value to index; the resulting index is then used to determine the point. Thus, a point scale’s values must be coercible to a primitive value, and the primitive domain value uniquely identifies the corresponding point. If domain is not specified, this method returns the current domain.
# point.range([range]) · Source, Examples
If range is specified, sets the scale’s range to the specified two-element array of numbers. If the elements in the given array are not numbers, they will be coerced to numbers. If range is not specified, returns the scale’s current range, which defaults to [0, 1].
# point.rangeRound([range]) · Source, Examples
Sets the scale’s range to the specified two-element array of numbers while also enabling rounding. This is a convenience method equivalent to:
point
.range(range)
.round(true);Rounding is sometimes useful for avoiding antialiasing artifacts, though also consider the shape-rendering “crispEdges” styles.
# point.round([round]) · Source, Examples
If round is specified, enables or disables rounding accordingly. If rounding is enabled, the position of each point will be integers. Rounding is sometimes useful for avoiding antialiasing artifacts, though also consider the shape-rendering “crispEdges” styles. Note that if the width of the domain is not a multiple of the cardinality of the range, there may be leftover unused space, even without padding! Use point.align to specify how the leftover space is distributed.
# point.padding([padding]) · Source, Examples
If padding is specified, sets the outer padding to the specified number which is typically in the range [0, 1]. If padding is not specified, returns the current outer padding which defaults to 0. The outer padding specifies the amount of blank space, in terms of multiples of the step, to reserve before the first point and after the last point. Equivalent to band.paddingOuter.
# point.align([align]) · Source, Examples
If align is specified, sets the alignment to the specified value which must be in the range [0, 1]. If align is not specified, returns the current alignment which defaults to 0.5. The alignment specifies how any leftover unused space in the range is distributed. A value of 0.5 indicates that the leftover space should be equally distributed before the first point and after the last point; i.e., the points should be centered within the range. A value of 0 or 1 may be used to shift the points to one side, say to position them adjacent to an axis.
# point.bandwidth() · Source, Examples
Returns zero.
# point.step() · Source, Examples
Returns the distance between the starts of adjacent points.
# point.copy() · Source, Examples
Returns an exact copy of this scale. Changes to this scale will not affect the returned scale, and vice versa.