integrate-adaptive-simpson

Compute a definite integral of one variable using Simpson's Rule with adaptive quadrature

Introduction

This module computes the definite integral

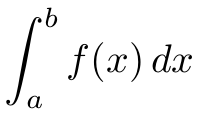
$\int_a^b f(x) \, dx$

using Romberg Integration based on Simpson's Rule. That is, it uses Richardson Extrapolation to estimate the error and recursively subdivide intervals until the error tolerance is met. The code is adapted from the pseudocode in Romberg Integration and Adaptive Quadrature.

Install

$ npm install integrate-adaptive-simpson

Example

To compute the definite integral

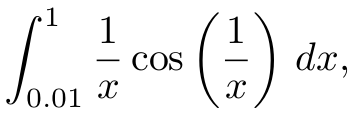
$\int_{0.01}^{1} \frac{1}{x}\cos\left(\frac{1}{x}\right)\,dx,$

execute:

var integrate = require('integrate-adaptive-simpson');
 
function f (x) {
  return Math.cos(1 / x) / x);
}
 
intiegrate(f, 0.01, 1, 1e-8);
// => -0.3425527480294604

To integrate a vector function, you may import the vectorized version. To compute a contour integral of, say, 1 / z about , that is,

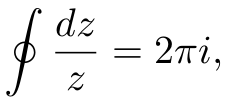
$\oint \frac{dz}{z} = 2\pi i,$

var integrate = require('integrate-adaptive-simpson/vector');
 
integrate(function (f, theta) {
  // z = unit circle:
  var c = Math.cos(theta);
  var s = Math.sin(theta);
 
  // dz:
  var dzr = -s;
  var dzi = c;
 
  // 1 / z at this point on the unit circle:
  var fr = c / (c * c + s * s);
  var fi = -s / (c * c + s * s);
 
  // Multiply f(z) * dz:
  f[0] = fr * dzr - fi * dzi;
  f[1] = fr * dzi + fi * dzr;
}, 0, Math.PI * 2);
 
// => [ 0, 6.283185307179586 ]

API

`require('integrate-adaptive-simpson')( f, a, b [, tol, maxdepth]] )`

Compute the definite integral of scalar function f from a to b.

Arguments:

f: The function to be integrated. A function of one variable that returns a value.
a: The lower limit of integration, .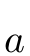
b: The upper limit of integration, .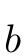
tol: The relative error required for an interval to be subdivided, based on Richardson extraplation. Default tolerance is 1e-8. Be careful—the total accumulated error may be significantly less and result in more function evaluations than necessary.
maxdepth: The maximum recursion depth. Default depth is 20. If reached, computation continues and a warning is output to the console.

Returns: The computed value of the definite integral.

`require('integrate-adaptive-simpson/vector')( f, a, b [, tol, maxdepth]] )`

Compute the definite integral of vector function f from a to b.

Arguments:

f: The function to be integrated. The first argument is an array of length n into which the output must be written. The second argument is the scalar value of the independent variable.
a: The lower limit of integration, .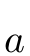
b: The upper limit of integration, .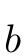
tol: The relative error required for an interval to be subdivided, based on Richardson extraplation. Default tolerance is 1e-8.
maxdepth: The maximum recursion depth. Default depth is 20. If reached, computation continues and a warning is output to the console.

Returns: An Array representing The computed value of the definite integral.

References

Colins, C., Romberg Integration and Adaptive Quadrature Course Notes.